対称群の部分群の簡単化(こどふぉブログ勉強月間1)

こどふぉブログ勉強月間では、 codeforces blog の積読を消化して、ついでに日本語の資料を作っておくことを目標にします。

参考資料

プログラムに実装するときに私は混乱したので、本投稿では、配列の考えで理解しやすいと思う書き方にしました。

対称群の部分群とは

$1$ 以上の整数 $n$ を固定します。 $(0,1,\ldots ,n-1)$ の要素を並べ替えて得られる列全体の集合を $S_n$ とします。 $s\in S_n$ であるとき、 $s$ の $k$ 番目(一番左は $0$ 番目として数える)の要素の値を $s[k]$ で参照します。

$a\in S_n$ , $b\in S_n$ に対して、 $(a[b[0]],a[b[1]],\ldots ,a[b[n-1]])$ を $ab$ と表します。つまり $(ab)[k]=a[b[k]]$ です。この 2 項演算によって、 $S_n$ は群になります：

  • $a\in S_n$ , $b\in S_n$ , $c\in S_n$ ならば $a(bc)=(ab)c$ です。
    (∵ $(ab)[c[k]]=a[b[c[k]]]=a[(bc)[k]]$)
  • $e=(0,1,\ldots ,n-1)$ は単位元です。
  • $a\in S_n$ に対して、 $a$ の逆元は $a^{-1}[a[k]]=k$ とすればとれます。

$S_n$ の部分集合 $A$ に対して、「 $a\in A$ , $b\in A$ , $ab\notin A$ となるような $a$ , $b$ を選び、 $ab$ を $A$ に加える」という操作を可能な限り繰り返して得られる集合 $A$ を $G$ とすると、これも群をなします。このとき $G=\langle A \rangle$ と表します。

問題

$S_n$ の部分集合 $A$ が与えられます。以下の条件を満たす $G_1,G_2,\ldots ,G_{n-1}$ ( $G_k\subset S_n$ )を求めてください。

  • $g\in G_k$ のとき、 $g[x]=x$ ( $k\lt x$ ) 。
  • $g\in G_k$ のとき、 $g[k]\neq k$ 。
  • $G_k$ の要素 $g$ 全体で、 $g[k]$ の値は相異なる。
  • 「$g_1\in G_1,g_2\in G_2,\ldots ,g_{n-1}\in G_{n-1}$ を用いて $g=g_{n-1}\cdots g_2g_1$ と表せる。」 $\iff$ 「 $g\in \langle A \rangle$ 。」

$\langle A \rangle$ の要素全体を、 $n-1$ 番目の要素から順に決定してゆく(*1)手順で表すことで、具体的な計算を DP で効率化することにつながります。全体は、 $O(n^6)$ 時間で計算できます。

(*1) $g[n-1]=g_{n-1}[ \cdots g_2[g_1[n-1]]\cdots ]=g_{n-1}[n-1]$ です。つまり、 $g[n-1]$ の値は $g_{n-1}$ のみに依存します。

A の要素を絞り込む

$A\subset S_n$ が与えられたとき、 $\langle A\rangle =\langle A^\prime\rangle$ かつ $|A^\prime|\leq n(n-1)/2$ となるような $A^\prime$ を、 $O(n^2|A|)$ 時間で求めます。

イメージ

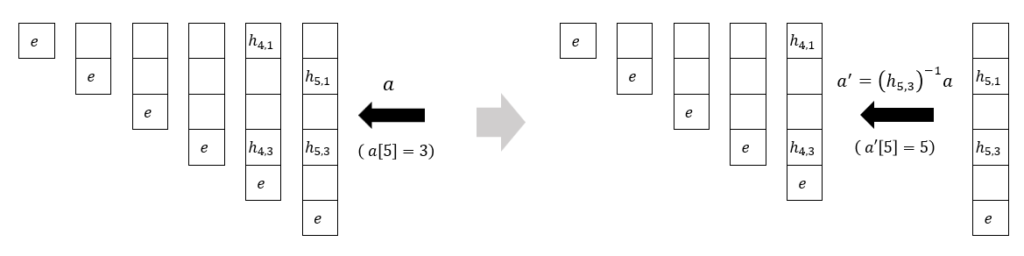
$0\leq j\lt i\lt n$ について、 $h_{i,j}\in S_n$ を、

  • $h_{i,j}=e$ または
  • ( $h_{i,j}[i]=j$ かつ $h_{i,k}=k$ ($i\lt k$) )

が成り立つようにとり、これで $A^\prime=\lbrace h_{i,j} \mid 0\leq j\lt i\lt n \rbrace$ となるようにします。このために、まず $h_{i,j}=e$ として、 $A$ の要素を $1$ つずつ、以下の手順で処理します。

  1. 取り出した要素を $a$ とします。
  2. $a[n-1]=n-1$ のときは $n$ が $1$ だけ小さい場合と同じ処理になります。
  3. $h_{n-1,a[n-1]}=e$ のときは、 $h_{n-1,a[n-1]}\leftarrow a$ と更新して終わりです。
  4. $h_{n-1,a[n-1]}\neq e$ のときは、 $a\leftarrow {h_{n-1,a[n-1]}}^{-1}a$ と更新すれば $a[n-1]=n-1$ となります。

全体の答えを出す

$A$ から $G_{n-1}$ を求め、さらに $A$ から $n-1$ 番目の要素が変化しない成分 $B$ を取り出すことで、 $n$ を減らしながら再帰的に処理できます。正確には、

  • $a\in \langle A\rangle \iff a\in \lbrace gb \mid g\in G_{n-1}, b\in B\rbrace$
  • $b\in B$ について、 $b[n-1]=n-1$

を満たすような $B$ を求めるということです。

def solve(A, n)
    A = reduce(A)     # 絞り込み

    G = [[] for _ in range(n)]
    for m in reversed(range(1,n)) :
        A, G[m] = solve_sub(A, n, m)
    return G

G[n-1] を求める

$G_{n-1}$ を求めます。つまり、 $k=0,1,\ldots ,n-1$ について、 $r_o[n-1]=o$ を満たすような $r_o\in \langle A\rangle$ が存在するかどうか、また存在するなら $1$ つ求める必要があります。

$r_o\in \langle A\rangle$ が存在する $o$ 全体の集合を $O_{\text{rbit}}$ とおきます。

常に $r_{n-1}=e$ ととれて、 $n-1\in O_{\text{rbit}}$ です。

$o\in O_{\text{rbit}}$ のとき、 $a\in A$ について $r_{a[o]}=ar_o$ ととれるため、 $a[o]\in O_{\text{rbit}}$ です。これを用いてグラフ探索の要領で $O_{\text{rbit}}$ および $G_{n-1}$ が求まります。

計算量は $O(n^2+n |A|)$ です。

B を求める

$\langle B\rangle =\lbrace p \in \langle A\rangle \mid p[n-1] \rbrace$ を満たす $B$ を求めます。

結論としては、 $B=\lbrace {r_{a[o]}}^{-1} a r_o \mid o\in O_{\text{rbit}} , a\in A \rbrace$ とすればよいです。

$p\in B$ について、 $p$ を $A$ の要素の積で表したとします。

$$p=a_0a_1a_2 \cdots a_{q-1}$$

$n-1$ が $t$ 番目の要素に移動するタイミングで $r_tr_t^{-1}$ を挟むことで、 $n-1$ を一旦もとの位置に戻します。

$$p= a_0 (r_{t_1} {r_{t_1}}^{-1}) a_1 (r_{t_2} {r_{t_2}}^{-1}) a_2 (r_{t_3} \cdots {r_{t_{q-1}}}^{-1}) a_{q-1}$$

つまり

$$p= (e a_0 r_{t_1}) ({r_{t_1}}^{-1} a_1 r_{t_2}) ({r_{t_2}}^{-1} a_2 r_{t_3}) \cdots ({r_{t_{q-1}}}^{-1} a_{q-1} e)$$

$$p= ({r_{n-1}}^{-1} a_0 r_{t_1}) ({r_{t_1}}^{-1} a_1 r_{t_2}) ({r_{t_2}}^{-1} a_2 r_{t_3}) \cdots ({r_{t_{q-1}}}^{-1} a_{q-1} r_{n-1})$$

よって、

$$B=\lbrace {r_\alpha }^{-1} a r_\beta \mid 0\leq \alpha\lt n , 0\leq \beta \lt n, a\in A , {r_\alpha }^{-1} a r_\beta[n-1]=n-1\rbrace$$

が条件を満たします。言い換えにより、

$$B=\lbrace {r_{a[o]}}^{-1} a r_o \mid o\in O_{\text{rbit}} , a\in A \rbrace$$

となります。 $B$ の要素数はおよそ $n|A|$ になりますが、これを絞り込みによって $O(n^2)$ 個に変形することで計算量は抑えられます。

まとめて完成

絞り込みにより、 $O(n^2|A|)$ 時間で $|A|$ が $O(n^2)$ である問題に帰着します。

$G_{n-1}$ を求めるのに $O(n^3)$ 時間かかります。 $|B|$ は $O(n^3)$ になり、その計算に $O(n^4)$ 時間かかります。これを再度絞り込みにかけると $O(n^5)$ 時間かかります。

よって、 $G_{n-1},G_{n-2},\ldots $ と順に求めてゆくと、 $O(n^6)$ 時間で目的のものが得られます。

タイトルとURLをコピーしました