First AC は嬉しいです。書きたいし、書かないよりいいので解説を書きます。
問題
yukicoder contest 285 F ★2.5 国勢調査(Easy)
問題リンク:https://yukicoder.me/problems/no/1420
要約:
$A \ \mathrm{xor} \ B$ は、 $A$ と $B$ のビットごとの排他的論理和です。
長さ $N$ で、要素が $0$ 以上 $2^{30}$ 未満の整数列 $X$ $(X_1, \dots ,X_N)$ について、 $M$ 個の制約が与えられる。制約をすべて満たす整数列 $X$ はあるか。あるなら例を示せ。
制約 $(i,j,y)$:$X_i \ \mathrm{xor} \ X_j=y$ 。
制約:
$N,M \le 10^5$
解説
連結な制約
制約によって $i$ から $j$ まで伝っていけるならば、 $X_i \ \mathrm{xor} \ X_j $ の値は一意。
制約 $(i,j,y)$ を、数列 $X$ の要素 $X_i$ と $X_j$ を結ぶ辺とした、無向グラフを考えると分かりやすいです。
制約を順番に追加することを考えます。今追加する制約 $(i,j,y)$ について、すでに追加された制約を伝って $i$ から $j$ まで行けるなら、 $y$ としてあるべき値 $X_i \ \mathrm{xor} \ X_j$ はすでに決定しています。
なぜなら、制約 $(u,v,a)$ と制約 $(v,w,b)$ によって $X_u \ \mathrm{xor} \ X_v=a,X_v \ \mathrm{xor} \ X_w=b$ がわかっているとき、 $X_u \ \mathrm{xor} \ X_w=a \ \mathrm{xor} \ b$ であり、制約 $(u,w,a \ \mathrm{xor} \ b)$ が従うからです (この流れを繰り返すと分かります)。
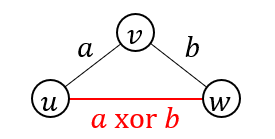
重み付き Union-Find
重みの差を $ \mathrm{xor} $ で計算するような重み付き Union-Find で制約を管理できる。
Union-Find は、無向グラフについて
- 無向辺の追加
- $2$ 頂点が連結か判定
を処理できますが、重み付き Union-Find はさらに、各頂点 $v$ に値 $V_v$ が割り当てられたとして
- 無向辺 $(i,j)$ を追加するとき、同時に $V_i-V_j=x$ を満たす “差” $x$ を設定する
- $2$ 頂点 $(u,v)$ が連結ならば、”差” $V_u-V_v$ を求める
ができます。
重み付き Union-Find の、
- 頂点を $X$ の要素
- 辺を制約の有無
- 頂点に割り当てられた値を $X$ の要素の値
- “差” $A-B$ を $A \ \mathrm{xor} \ B$
とすれば、制約をすべて管理できます。
制約 $(i,j,y)$ を追加する際、もし $i,j$ が連結、つまり既に $X_i \ \mathrm{xor} \ X_j$ の値がわかるとき、
- $y \ne X_i \ \mathrm{xor} \ X_j$ なら、数列 $X$ は存在しない。
- $y=X_i \ \mathrm{xor} \ X_j$ なら、その制約はなかったことにできる。
となります。
仮に制約を最後まで追加したとします。各”連結な制約“ごとに、 $X$ のある要素 $X_s$ を $X_s=0$ とすると、制約 $(s,i,y)$ によって $X_i=y$ が決まります。これは全制約(問題全体の制約を含めて)を満たすので、これで $X$ が構築できます。
まとめ
制約の内容に従って重み付き Union-Find を操作すれば答えが求まります。
僕の Union-Find の実装はパス圧縮で、クエリ当たり $ \mathrm{amortized}\ O ( \log N )$ なので、全体の時間計算量は $O((N+M) \log N)$ です。
提出コード
提出コードのリンク:https://yukicoder.me/submissions/625512
余談
Hard が Easy の上位互換じゃないのは先入観に反しました。