(2021/7/10 更新)
公式解説のヒント1が超強力。
問題
AtCoder Grand Contest 052 B – Tree Edges XOR
問題リンク:https://atcoder.jp/contests/agc052/tasks/agc052_b
解説
注意:一部で僕の思考過程を再現しながら解説します。最短ルートとは限りません。
操作を単純に
頂点に重みをつけると、操作は隣接頂点の重みのスワップになる。
問題文中の操作をやってみましょう。重み $x$ の辺 $(u,v)$ を選ぶとすると、赤い辺の重みが XOR $x$ されます。
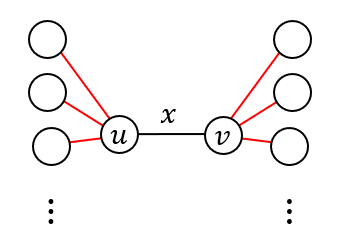
頂点 $u,v$ に接続する辺のほぼ全ての辺に XOR $x$ されているように見えます。ここで、頂点に重みをもたせ、「接続する辺すべての重みがこの重みで XOR される」と意味を持たせます。すると、操作は「頂点 $u,v$ それぞれの重みに XOR $x$ する」ことと同じになります。
頂点 $i$ の重みを $V_i$ と表します。辺 $(u,v)$ の元の重みが $0$ として、その辺に操作をすると、 $V_u$ は $V_u$ XOR $(V_u$ XOR $V_v)$ に、つまり $V_v$ になります。同様に $V_v$ は $V_u$ になるので、全体では $V_u$ と $V_v$ が入れ替わることになります。
初期状態で全頂点にうまく重みをつければ、辺の重みを考えないようにできるでしょうか。頂点 $1$ の重みを $0$ とすれば、辺を伝って全頂点の重みがちょうど決定し、初期状態を再現できます。この重みは公式解説のヒント1における「頂点 $1$ との距離」と同じです。
不変量
初期状態での頂点 $i$ の重みを $a_i$ 、目的の状態での頂点 $i$ の重みを $b_i$ とします。
答えは、 $b$ の全要素を任意の値 $W$ で XOR してよいとして、 $a$ と $b$ を集合として比べること。
操作による頂点の重みの変化の不変量を探します。
操作が隣接要素のスワップなので、値の集合はほぼ一定で、逆に一定であればどの順列も再現できます。例外は頂点 $1$ の重みが $0$ 以外( $W$ とおく)になるときです。このときは $b_1=W$ として $b$ を再計算して比べればよいです。どんな $W$ を取ったとしても、 $a$ と $b$ が集合として一致してしまえば実現可能なので、上の緑の題が示されます。
$W$ の特定
$b_1$ を $b_1$ XOR $W$ で置き換えて $b$ を再計算ときの $b$ の変化は、 $b$ の要素すべてを $W$ で XOR することに他なりません。 $N$ は奇数なので、このとき $b$ 全要素の XOR は、 $W$ で XOR されます。したがって、 $a$ と $b$ それぞれ全要素の XOR をとって比べれば $W$ の値が特定できます。
まとめ
$W$ を特定し、 $b$ (または $a$ ) の全要素を XOR $W$ し、 $a$ と $b$ を集合として比べればよいです。集合として比べるときは、ソートしてから列として比べればよいです。
計算量は $O(N \log N)$ です。
提出コード
提出コードのリンク:https://atcoder.jp/contests/agc052/submissions/20756618
$W$ の特定が雑なので、計算量に $O(N \log C)$ ( $C$ は $w^1_i,w^2_i \lt C$ の $C$ で今回は $2^{30}$ ) が足されます。