マラソンは下手ですが、「全く手が出せない」なんてことはありません。
暫定テストの最終得点: $48,092,333,451$

問題
AtCoder Heuristic Contest 001 A – AtCoder Ad
問題リンク:https://atcoder.jp/contests/ahc001/tasks/ahc001_a
注意
得点率とは、各テストケースで $10^9$ 点に対してどれだけの割合の点数が取れるかの目安です。シードを $0$ から $99$ として生成した $100$ 個の入力で実行し、その結果を平均して求めています。暫定テストは無関係です。
解説 (手抜きルート)
得点率 $ 0.0021 \% $
極端な話、長方形の面積が $1$ だとしても微小なスコアが得られます。
algo風問題:
次の条件を満たすような答えを $1$ つ求めてください。
- 長方形 $i$ は点 $(x_i+0.5,y_i+0.5)$ を含む
- 各長方形の面積は $1$
答えは $(a_i,b_i,c_i,d_i)=(x_i,y_i,x_i+1,y_i+1)$ です。
たったこれだけのことですが、点数は必ず正になるので、 $0$ 点には勝てます。
提出コード:https://atcoder.jp/contests/ahc001/submissions/20753272
得点率 $ 0.83 \% $
面積が $1$ だとどうしてもこれ以上良いスコアは出ないので、次は逆に面積を保証します。目標面積の総和の制約から、目標面積は $1$ 個あたり $10000 \times 10000 / n$ くらいのはずです。
algo風問題:
$10000 \times 10000$ のマス目を、長方形に分けて大体 $n$ 等分してください。
平行に $n-1$ 回スライスするだけです。とりあえず長方形 $i$ は $(a_i,b_i,c_i,d_i)=( \lfloor 10000i/n \rfloor ,0, \lfloor 10000(i+1)/n \rfloor ,10000)$ です。(そんな広告は嫌だ)
あとは割り当てですが、難しいので思い切ってこのままの順番で割り当てます。長方形 $n$ 個中 $1$ 個くらいは当たります。
提出コード:https://atcoder.jp/contests/ahc001/submissions/20688469
得点率 $ 42 \% $
さっき放棄した割り当てを考えます。目的の点を含む長方形を増やせば、得点が増えます。この数を最大化しましょう。
algo風問題:
さっきの方法で分けた長方形を企業に割り当てて、目的の点を含む長方形の数を最大化してください。
長方形内に目的の点が $1$ つも含まれなければ、その領域は放棄します。そうでなければ、目的の点のうち $1$ つを満たすようにし、他は放棄した領域に割り当てます。
提出コード:https://atcoder.jp/contests/ahc001/submissions/20808983
得点率 $ 60 \% $
さっきの割り当てのうち、目標面積より大きい長方形を割り当てているものは、その長方形を小さく変えるだけで得点が増えます。次の問題を考えます。
algo風問題:
長方形とその内部の点が与えられます。元の長方形に収まる長方形で、面積が大体 $r_i$ で点 $(x_i,y_i)$ を含むものを求めてください。
元の長方形は $x$軸方向に短いので、 $y$軸方向に調整し、長さ $r_i \div $(幅) で $y_i$ を含むものが良いです。長さ $r_i \div $(幅) の区間を適当にとって目的の点を含むまで平行移動しましょう。
上を踏まえると、目標面積は小さいほうが都合がよいです。ならば、長方形に対応させる目的の点は、目標面積が最小のものを選びます。
提出コード:https://atcoder.jp/contests/ahc001/submissions/20812501
解説 (本気ルート)
手抜きルートでは、目的の点を無視するかもしれない運任せを考えました。しかし、例えば得点率 $ 99 \% $ を取るには少なくとも $ 99 \% $ の割合で目的の点を含む必要があります。それならば、目的の点はすべて確保した状態で、面積を調整するのが良さそうです。
得点率 $ 53 \% $
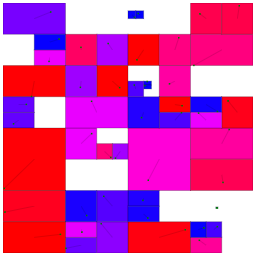
ある程度の面積を確保しつつ、重ならないような長方形の配置を求めましょう。手抜きルート後半でやったように、全体の領域を $n$ 個にスライスたような配置で、目的の点を含められるものは含めましょう。問題は、スライス後の $1$ つの領域に目的の点が複数含まれる場合です。しかしこれは縦横比は違えど初めと同じ問題になります。再帰的にスライスしましょう。再帰的に、かぁ……。嫌だなぁ、実装。
どうせ再帰的に領域を分割するのなら、 $n$ 分割でなく $2$ 分割にします。正方形に近いほうが後々の改善が柔軟になりそうなので、分割は領域が正方形に近くなるように行います。以上をサンプル入力で行い、ビジュアライザに通すと右が得られます。
提出コード:https://atcoder.jp/contests/ahc001/submissions/20781437
得点率 $ 83 \% $
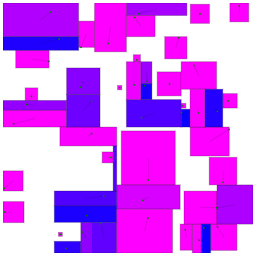
手抜きルートでもやったように、大きすぎる長方形は小さくします。高さだけ調整するのでもよいですが、幅と高さを両方調整しても同じアルゴリズムを $2$ 回行うだけです。後者だと正方形に近い形が維持できますね。これだけで $ 71 \% $ まで伸びます。
前パートの画像の右下あたりに点のようなものがあるのがわかるでしょうか。複数の目的の点がうまく分割されずに領域がかなり細かくなってしまっています。これを防ぐため、複数の点は確実に分割します。僕は、分割の線を選ぶ際の条件を、全体の領域の形のかわりに「目的の点をすべて含む最小の長方形」で置き換えて考えました。以上 $2$ つによって、得点率は $ 83 \% $ になります。
提出コード:https://atcoder.jp/contests/ahc001/submissions/20840756
得点率 $ 94.0 \% $
空き面積がもったいないので、面積が足りてない長方形を伸ばします。伸ばせるかの判定はどうすればよいですか?伸ばした時にほかの長方形と衝突しないか判定すればよいです。伸ばした長方形と各長方形の衝突を判定するので計算量は $O(n)$ です。しかし、伸ばす長さを決め打つのは効率が悪そうです。代わりに「どれだけ伸ばせるか」を求めたいですが、これも同じようにして計算量 $O(n)$ でできます。

ランダムに長方形と伸ばす向きを選び、「どれだけ伸ばせるか」を求め、それをもとに(いい感じに)少しずつ伸ばすことを繰り返します。 $10^6$ 回くらいはできます。
もし既に面積が足りていたり、変形によって面積がオーバーしたりする場合はどうでしょう。僕は、一度面積をオーバーしても良いことにし、直後に面積を再調整することにしました。面積が足りている長方形も変形する可能性があり、より多くのパターンが試せると考えられます。
提出コード:https://atcoder.jp/contests/ahc001/submissions/20840365
得点率 $ 94.3 \% $
面積は後から増やせることがわかりました。今まで元の面積を大きくしていましたが、それだと密度が上がって後の自由度が下がります。元の面積を小さめにしましょう。これまでの方法は長方形が細長くなりやすいので、元の長方形を正方形に近づけました。
提出コード:https://atcoder.jp/contests/ahc001/submissions/20805675
得点率 $ 96.1 \% $
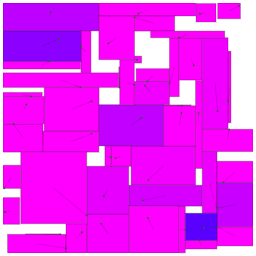
上の方法だと、一度長方形がぴったり接してしまうと変形の自由度が極端に下がります。実行時間が余っているので、状態の一部を破壊してその部分だけやり直す試行をします。得点が増加したら変化を適用します(山登り法)。
細かい手順を決めていきます。破壊する部分はまとまった位置関係がよさそうなので、ランダムに選んだある点とのマンハッタン距離が小さい順に $K=5$ 個選んで破壊しました。破壊は、正方形に近い小さい形に調整することにしました。やり直しは、全体に対して行う改善と同じものを $K$ 個の長方形のみに行いました。
提出コード:https://atcoder.jp/contests/ahc001/submissions/20922971