おことわり
実際にプログラムを書こうとしたときに感じたことを「だいたいこうなんだろうな」という感じで書きます。本当にすべてのケースで正しく動くか、とにかく怪しいですし、記事がいらなくなったら消します。
私がよく参考にしたのは [2] と [3] ですが、論文を参照するなら [1] の Preliminaries が良いのではないでしょうか。
準備
DFS 木の辺を tree arc 、後退辺を frond といい、これらを組み合わせたグラフを palm tree というらしいです。
アルゴリズム全体
アルゴリズムです。論文に準じますが、実際の実装に変換しやすくしたいので、一度すべて書き直します。あと Q-node は明示的には作らないものとします。
PathSearch(v) :
for e in copied Adj(v) :
w = e.to
if e.isTreeEdge :
if e.startingPath :
deletedHAB = pop (h,a,b) from TSTACK while a > w.lowpt1
if deletedHAB.empty : TSTACK.push( (w + w.nd - 1, w.lowpt1, v) )
else :
y = max h for (h,a,b) in deletedHAB
TSTACK.push( (max(y, w + w.nd-1), w.lowpt1, deletedHAB.last.b) )
TSTACK.push(EOS)
PathSearch(w)
ESTACK.push(w.treeArc)
# BEGIN : check for type-2 pairs
while v != ROOT and (TSTACK.top.a == v or w.degree == 2 and FirstChild(w) > w)
(h,a,b) = TSTACK.top
if a == v and b.parent == a : Tstack.pop()
else :
x = NIL
eab = NIL, ep = NIL
if w.degree == 2 and FirstChild(w) > w :
x = FirstChild(w)
vw, wx = poped 2 edges from ESTACK
C = NewComponent({ vw, wx })
ep = newVirtualEdge(v, x, C)
if ESTACK.top.is(v,x) : eab = ESTACK.pop
else :
TSTACK.pop
C = NewComponent({})
while ESTACK has an edge (x,y) and (a <= (x, y) <= h) :
if ESTACK.top.is(a, b) : eab = ESTACK.pop()
else : C.addEdge(ESTACK.pop())
ep = NewVirtualEdge(a, b, C)
x = b
if eab != NIL :
C = NewComponent({ eab, ep })
ep = NewVirtualEdge(v, x, C)
ESTACK.push(ep)
MakeTreeEdge(ep)
w = x
# END : check for type-2 pairs
# BEGIN : check for type-1 pairs
if w.lowpt2 >= v and w.lowpt1 < v and v.parent != ROOT :
C = NewComponent({})
while ESTACK has an edge (x,y) and (w <= (x, y) <= w + w.nd) :
C.AddEdge(ESTACK.pop)
ep = NewVirtualEdge(v, w.lowpt1, C)
if (not ESTACK.empty) and ESTACK.top.is(v, w.lowpt1) :
C = NewComponent({ ESTACK.pop, ep })
ep = NewVirtualEdge(v, w.lowpt1, C)
if w.lowpt1 != v.parent : ESTACK.push(ep)
else :
C = NewComponent({ ep, v.treeArc })
ep = NewVirtualEdge(w.lowpt1, v, C)
MakeTreeEdge(ep, w.lowpt1, v)
# END : check for type-1 pairs
if e.startingPath :
while TSTACK.top != EOS : TSTACK.pop()
TSTACK.pop()
while TSTACK has (h,a,b) and a != v and b != v and High(v) > h :
TSTACK.pop()
else : # not e.isTreeEdge
Visit(e)
if e.startingPath :
deletedHAB = pop (h,a,b) from TSTACK while a > w
if deletedHAB.empty : TSTACK.push( (v, w, v) )
else :
y = max h for (h,a,b) in deletedHAB
TSTACK.push( (y, w, deletedHAB.last.b) )
if w == v.parent :
C = NewComponent({ e, v.treeArc })
ep = NewVirtualEdge(w, v, C)
MakeTreeEdge(ep, w, v)
else : ESTACK.push(e)
Decompose(N, E) : # the graph is biconnected and N >= 3
Replace parallel edges with a virtual edge of P-node
Calclate the palm tree
Reorder the adjacency lists
Recalclate the palm tree
PathSearch(ROOT)
for C in TheComponents of unknown type :
if C.edges.size != 3 : C.type = "R"
else if C is parallel edges : C.type = "P"
else : C.type = "S"
for C1 in TheComponents if C1.type == "P" or C1.type == "S" :
for a virtual edge e in C1.edges :
C2 = another component than C1
Delete(e)
Merge C2.edges into C1.edges
Delete(C2)実装改善のための考察・理解
std::list や再帰関数、 std::vector を自由に使って本当に愚直に実装すると、メモリ効率が大変になります。
PathSearch は DFS 木に沿った深さ優先探索です。また、 ESTACK に辺が追加される順番は帰りがけ順です。辺が削除・追加されても、隣接リストをソートした DFS 木としての性質は保つので、頂点の番号および v.lowpt1, v.lowpt2, v.nd, e.startingPath は PathSearch 内で変更されません。辺が削除候補になるのは帰りがけ順なので、走査前に Adj をコピーしてもかまいません。逆に、例えば双方向連結リストで実装してコピーしないで操作すると、今見ている辺が削除されることがあるので失敗する場合があります。
ep や eab でガチャガチャやっているのは新しくできた多重辺の処理です。これにより PathSearch 中でグラフは単純を保ちます。
check for type-2 pairs
type-2 を 2 種類に分けて処理しています。いろいろ簡略化したイメージがこれです。
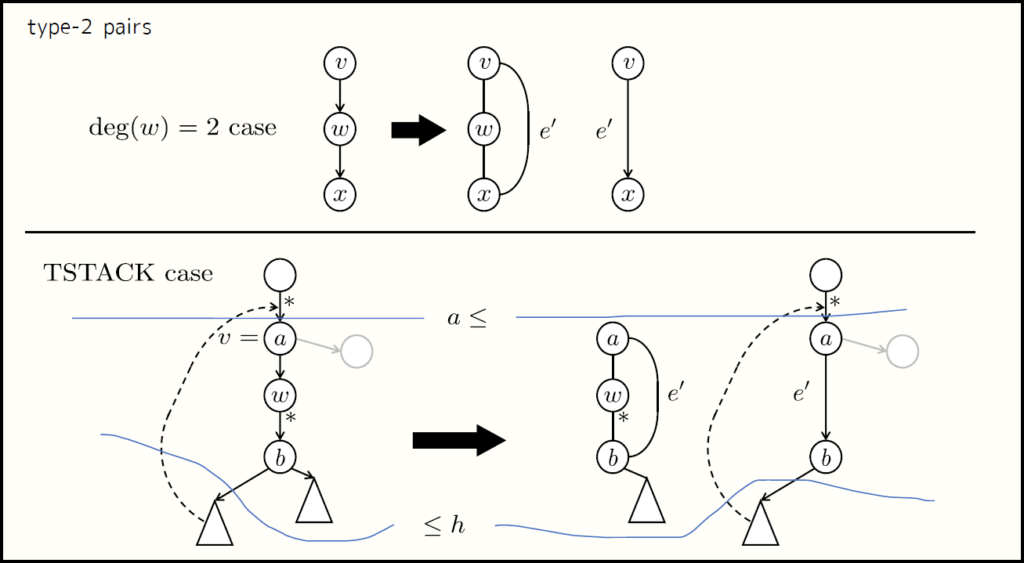
グレーはまだ訪れていない部分を表します。
check for a type-1 pair
type-1 を処理しています。いろいろ簡略化したイメージがこれです。
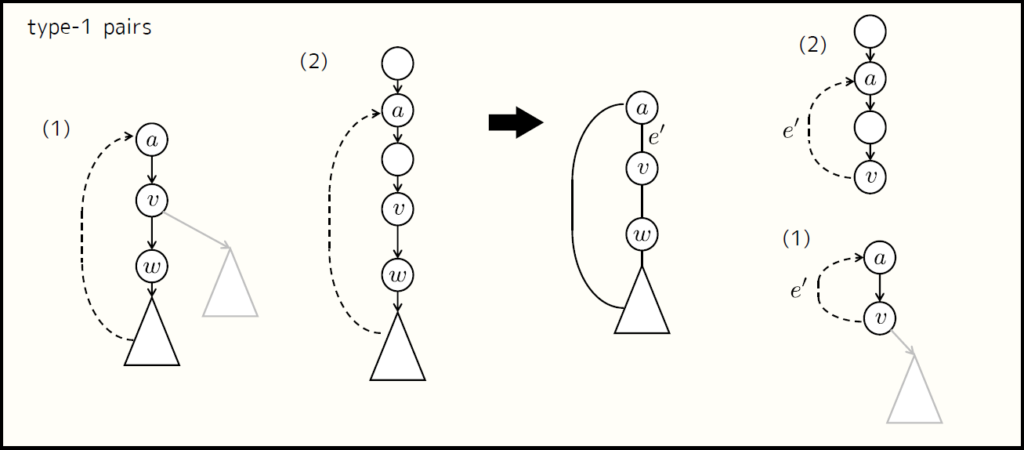
FirstChild(w) の計算
$\text{FirstChild}(w)$ が呼ばれているのは $\text{deg}(w)=2$ の場合のみです。これは $w$ の唯一の子が木の辺であるかどうかの判定に他なりません。このためには隣接リスト Adj を完全に動的に管理する必要はなく、削除を遅延できます。すなわち必要な Adj は stack で実装できます。単方向連結リストでもよいでしょう。さらに、木の辺のみ見ればよいので、 frond を追加する必要がありません。
High(v) の計算
$v$ に入ってくる frond のリスト $F(v)$ では削除を遅延できます。
type-1 の処理で生じた frond を $F(v)$ のどこに入れればよいかの問題がありますが、改良された隣接リストのソート関数 $\phi$ において
- 追加されるのは $3w+1$ のケースであること
- これよりも前に訪れる $3lowpt1(w)+2$ のケースはすべて type-1 に該当すること
を考慮すると $e^{\prime}$ は最後に訪れられているべき辺の $1$ つになるので、末尾に入れていればよさそうです(本当?)。これを信じると deque や単方向連結リストで実装できます。
たぶんソート関数 $\phi$ の改良の動機は、 ESTACK の末尾に $e^{\prime}$ や元から存在した $v\hookrightarrow a$ が追加されたときに多重辺になっているのを検知するためではないでしょうか。
NewComponent と NewVirtualEdge と MakeTreeEdge
type-2 のときの virtual edge は新しい tree arc に、 type-1 のときは新しい frond になります。このように、 virtual edge 追加時に tree arc か frond かが決まるので、 NewVirtualEdge にフラグの引数を追加すれば MakeTreeEdge は不要です。すると Adj の付け替えが不要になります。そもそも後述のように frond 追加時は Adj への追加が不要なので重要ではなさそうです。
また、成分の切り離しに対応して virtual edge を追加するので、 NewComponent に NewVirtualEdge を吸収することもできます。
再帰関数の排除
DFS 木に沿った探索なので、次のように再帰関数を排除できます。
DFS(root) :
ret = False, v = root, e = NIL
while v != NIL :
e = Adj[v][Itr[v]]
if ret :
# after returning from a tree edge
else :
if e.isTreeEdge :
# before going along a tree edge
v = e.to, ret = False
continue
else :
# when visiting a frond
Itr[v] += 1, ret = False
if Itr[v] == Adj[v].size :
v = v.parent, ret = True辺の追加削除、成分の追加削除
全体の結果に対する辺や成分の削除は、 PathSearch 終了後の処理でしか起こりません。明らかに、双方向連結リストは不要です。
例の怪しい実装
$3$ 頂点以上の biconnected なグラフ限定

今持ってるサンプルグラフでは PathSearch よりも前計算が遅いです。