paizaレーティングとは
paiza のスキルチェック問題に取り組んだ結果から計算される数値です。計算のための理論がある程度公開されています。 paizaレーティングの仕様はすべてこの文献の内容を参考にします。ただし、グリコレーティングの計算式は辻褄が合う解釈ができなかったので、 Wikipedia のほうを信用しました。たぶん裏でうまく係数を付けているのだと思いますが、今はその数学をやるための時間がないので…。
スキルチェック問題とは
paiza にログインすることで利用できるシステムです。スキルチェックというところに多数の問題が収録されており、各問題について
- 問題の名前
- 正答率
- ランク( D,C,B,A,S 、右のほうが難しい)
- 難易度( $r \pm rd$ の形式で書かれている )
を見ることができます。
また、問題に挑戦することで、問題の具体的な内容を確認できます。これに対して、適切に標準入出力を操作するプログラムを提出することで正誤判定が自動で行われます。
正解であれば、その問題の「ランク」を手に入れることができます。
また、問題の難易度と正誤に応じて挑戦者の「 paizaレーティング」が変動します。レーティングは通常の値 $r$ と偏差 $rd$ の $2$ つの値からなり、 $r \pm rd$ と表されます。さらに、このとき問題の難易度も paizaレーティングとほぼ同様の仕組みで変化します。問題のランクは変化しません。
paizaスキルチェックの難易度
AtCoder top60 程度の実力があれば、収録されている高難度問題であっても手も足も出ないほどの問題はありません。(間違えた問題もすべて復習して正解しているため、これは私のスキルチェックの結果を仮にすべて投稿したうえで統計をとればわかるので、実質的に公開情報の事実です。)
AtCoder と paiza は当然、対象実力層にずれがあります。そもそも十分すぎるレーティングをもってなお AtCoder に参加する集団は paizaスキルチェックのようなものを( FPS ゲームのような)娯楽として継続するような学生/社会人が私含め多数存在しますから、本当にわけが違います。
AtCoder のレーティングとの類似/相違
そもそも AtCoder とスキルチェックではルールが大幅に異なるため、必要となるレーティングシステムの制約も変わってくることでしょう。特に、スキルチェックでは人対人の相対評価が不可能なので、一度問題の難易度を評価する必要があります。
類似点として、実力保証としての側面が強いために「内部レーティング/表示レーティング」の概念が存在するという点があります。 AtCoder では内部レーティングから既定の値を差し引いて表示レーティングとされ、この既定の値がレーティング更新回数の増加に応じて漸近的に $0$ になるという仕様になっています。一方 paizaレーティングでは、内部レーティングの開始点をずらしたうえで、ある期間は問題のレーティングへの寄与を遮ることで対応しています。
また、どちらも複雑な計算式が利用されています。 AtCoder のものは「イロレーティングをベースにしているものの、多数の改造が加わっているためもはや原型はほとんどない。(AtCoderのレート計算式 | Qiita@anqooqie)」という評価があるほどです。
一方で、レーティングの再現性という観点では相違点が多いです。憶測が混じりますが、
- AtCoder のレーティングは一斉に行われるコンテストで決まるため、まったく同じ成績であると仮定すれば同じレーティングが算出される。しかし、各コンテストは一度限りなので、「まったく同じ成績」というものは後からは作れない。
- paizaスキルチェックでは、各人の取り組みに応じて問題のレーティングが変化しうる。後から、ある人と同じ問題に取り組んで同じ正誤状況が得られる可能性はあるが、それでも同じレーティングが算出されるとは限らない。
と考えることができます。
挑戦は 1 度限り
paizaスキルチェック に収録されている問題の数と難易度には限りがあります。そもそも paiza に収録されている問題の難易度の最大値は $2540\pm 21$ (執筆時 2023/07/10 A025 動物の体調管理、なんと S ではなく A ランクの問題)であるため、少し進んだ後はひたすら、いわゆる「格下」と戦う必要があります。
しかし、相手がいくら格下でも、勝率を $100.0 \%$ にできるとは限りません。なぜなら、ほぼ全問題を通して発生の可能性があるようなバグの要因があり(配列外参照など)、そのリスクは指数オーダーで減少するようなものではないからです。例えば、 AtCoder Beginner Contest の E 問題(Rating $1200$ 相当)で一回で正答を出す確率が $90 \%$ だからといって、 B 問題(Rating $100$ 相当 )を $99.9 \%$ の確率で一回で正答を出せるわけではありません。
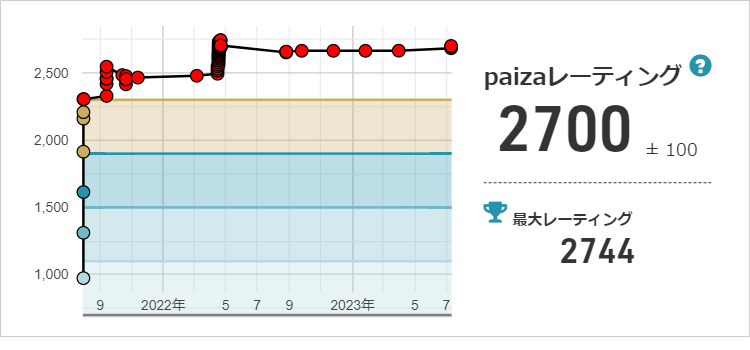
もう一度レーティングのグラフを見てみましょう。

赤の点が最も集中しているところは $33$ 連続正解と $1$ 回の不正解です。
こういうわけで、十分な実力があれば、最も難易度の表示が高い問題から順に挑戦するメリットがあると言えます。ただし、挑戦した問題は二度と帰ってきません。
言いたいことは、挑戦するうちにどんどん分が悪くなっていくということです。
心理的負荷
レーティング $2700$ を突破したあたりのオッズは、勝つと $+3$ 、負けると $-50$ です。
paizaスキルチェックは人生で一度のみ許された挑戦であり、その中でテストケースに対して出力が変化するようなバグを $1$ つ入れて提出した時点で脱落です。目が冴えます。
2800 (赤 paizaスキルチェックer )は可能なのか?
AtCoderer しか喜ばないだろ
レーティングの計算式はわかっているので、 Web ページから問題難易度を抽出したものから計算することで一応理論上の値を出すことができると考えました。
Wikipedia のグリコレーティングの計算式および paizaスキルチェック特有の初期値を用いて計算します。ただし、レーティング偏差の減少は $100$ で単純に打ち止めと仮定します。このとき、 S ランクの問題を難易度の高い順に $10$ 問連続正解すればレーティング $2809 \pm 158$ (四捨五入)を達成できると計算されました。アカウント登録即時に作戦開始する仮定の下では案外壮大ではないものなのかもしれません。
| $r_1$ | $RD_1$ | $r$ | $RD$ |
|---|---|---|---|
| 700 | 350 | ||
| 2526 | 56 | 1394 | 350 |
| 2488 | 29 | 2090 | 349 |
| 2478 | 32 | 2555 | 300 |
| 2446 | 39 | 2662 | 232 |
| 2436 | 45 | 2714 | 204 |
| 2415 | 39 | 2745 | 188 |
| 2415 | 23 | 2768 | 177 |
| 2396 | 16 | 2785 | 169 |
| 2367 | 27 | 2798 | 163 |
| 2365 | 40 | 2809 | 158 |
ただしこの検証にも大変な問題点があって、計算式が実際のものと同じ挙動をするかが非常に疑わしいです。問題の難易度が刻々変化していて、実例と突き合せた検証もままなりませんでした。
実際に実行してみたい気もしますが、もはや私自身では試せません。
個人プレーのデスゲームのような何か
私はレーティング自己べをこれ以上上げるのは困難になってしまいました。
腕(と注意力)に覚えがあるあなたは自身の限界に挑戦してみてはいかがでしょうか。(控えめの声)