2023/08/02 誤りを修正し、少し文を足しました。
問題提起
SSRS さんがツイートされていました。
問題
AtCoder Regular Contest 156 C – Tree and LCS 問題文
$T$ は与えられる木、 $N$ はその木の頂点数、 $P$ はコンテスタントが出力する順列でした。ジャッジは、 $P$ の類似度が $1$ であるかどうかを判定しなければなりません。
つまり、 $Q_{P_x}=x$ としてある $2$ 頂点の順序付きの組 $(u,v)$ であって、 $u$ , $v$ をこの順に含み、かつ $Q_u$ , $Q_v$ をこの順に含むような単純パスが存在してはいけません。
そのような単純パスは $u$ , $v$ , $Q_u$ , $Q_v$ (いくつかが同じ頂点を指す場合がある)を含みますが、その順番は次の $6$ 通りです。
- (1a) $u\rightarrow v\rightarrow Q_u\rightarrow Q_v$
- (2a) $u\rightarrow Q_u\rightarrow v\rightarrow Q_v$
- (3a) $u\rightarrow Q_u\rightarrow Q_v\rightarrow v$
- (3b) $Q_u\rightarrow u\rightarrow v\rightarrow Q_v$
- (2b) $Q_u\rightarrow u\rightarrow Q_v\rightarrow v$
- (1b) $Q_u\rightarrow Q_v\rightarrow u\rightarrow v$
ただし、 ” $\rightarrow$ ” は $0$ 本以上の辺をたどることを表します。
対称性( $u$ と $v$ を入れかえて前後反転するものと、 $x$ と $Q_x$ を入れ替えるもの)より、 (1a) と (2a) と (3a) のみ処理できればよいです。
時間計算量は $O(N \log N)$ です。
以降で使う表現のショートカット
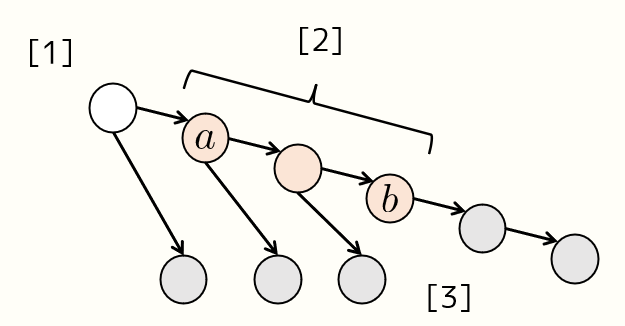
$a$ , $b$ を木 $T$ の頂点としたとき、部分木 $a\rightarrow b$ とは、
- $\text{dist}(a,x)-\text{dist}(b,x)=\text{dist}(a,b)$ を満たす頂点 $x$ を集めたものを頂点集合とする部分木
である。
木上の汎用テク
- LCA
- level ancestor problem
- $\text{median}(x,y,z)$ : $3$ 頂点の median とは、 $3$ 頂点からの距離の和が最小になるようにとった頂点のことで、木であれば一意です。任意の根に対して $\text{LCA}(x,y), \text{LCA}(y,z), \text{LCA}(z,x)$ を計算した結果から計算できます。
微妙に重要な変形
「木のいくつかの頂点が、 $1$ つのパス上にこの順に含まれている」という条件を処理する方法です。
ある木に含まれる $k$ 個の頂点 $a_1,a_2,\ldots ,a_k$ (重複可能)をとったとき、これらの頂点がある単純パスにこの順番で現れるためには、 $3\leq i\leq k$ を満たす整数 $i$ すべてで $\text{median}(a_1,a_{i-1},a_i)=a_{i-1}$ を満たすことが必要十分である。
$\text{median}(a_1,a_2,a_3)=a_2$ の場合、 $a_1$ , $a_3$ を通る単純パスは $a_2$ も通ります。さもなければ、 median から見て $a_1$ に近づく方向と $a_3$ に近づく方向が一致し、その方向に動くと距離の和が小さくなります。
(1) $\Rightarrow$ (必要性): $k=3$ の場合と同じです。
(2) $\Leftarrow$ (十分性): $i=3$ の条件によると、 $a_1,a_2,a_3$ を順に通る単純パス全体は、 $a_1$ と $a_3$ を通る単純パス全体に他なりません。よって、 $a_1,a_3,a_4$ を順に通る単純パスは $a_1,a_2,a_3,a_4$ を順に通ることが保証されます。同様に、数学的帰納法で一般の $k$ について示せます。
そのうえで、「 $\text{median}(x,y,z)=y$ 」は
- 「頂点 $y$ は $x$ , $z$ 間の単純パス上にある」
- 「頂点 $z$ は部分木 $x\rightarrow y$ に含まれる」
と言い換えることができます。
(1a) $u\rightarrow v\rightarrow Q_u\rightarrow Q_v$
$u$ を固定すると、そのようなパスが存在する組 $(u,v)$ の条件は
- $v$ は $u$ , $Q_u$ 間単純パスに含まれていて、かつ
- $Q_v$ は部分木 $u\rightarrow Q_u$ に含まれる
と表せます。それぞれ、「 $u$ に関する一点加算(事前に計算する)」と「 $v$ に関する区間和クエリ」からなる一点加算区間和の問題に変換することで、組 $(u,v)$ を $v$ ごとに数え上げる過程を $2$ 次元の区間和クエリに帰着します。
$T$ のオイラーツアーを取ったとします。いま、 $2$ 頂点 $a,b$ が与えられたとき、「 $x$ は部分木 $a\rightarrow b$ に含まれる」を満たすような頂点 $x$ の集合は、オイラーツアーの行きがけ順のうち $2$ 個以下の区間で表せます。よって、そのような頂点は区間和クエリで数え上げられます。
次に、「 $x$ は $a$ , $b$ 間の単純パスに含まれる」を変形します。オイラーツアーの始点を根 $r$ としたときの $a$ , $b$ の LCA を計算しておくことで、定数個の「 $x$ は $a$ , $b$ 間の単純パスに含まれる( $a$ は $b$ の祖先)」に変形されます。これは、ありうる状態を
- [1] $x\neq a$ かつ、 $a$ は部分木 $r\rightarrow x$ に含まれる
- [2] ( $x=a$ であるか、 $a$ は部分木 $r\rightarrow x$ に含まれない) が、 $b$ は含まれる
- [3] $b$ は部分木 $r\rightarrow x$ に含まれない
の $3$ つに分類したときの [2] と同じです。
よって、「$s_i$ が部分木 $r\rightarrow x$ に含まれるときに答えに $w_i$ を加算する」というクエリなどに分解されます。必要なクエリは、オイラーツアーの行きがけ順において $x$ に関する区間加算と $s_i$ に関する一点取得の形です。ここで差分列を管理することにすると $x$ に関する一点加算と $s_i$ に関する区間和に変形されます。
以上、 $2$ つの条件がそれぞれ適切な区間和クエリに変形されました。
各 $u$ に関して適切に点を配置したのち、 $v$ に関する区間和クエリをオフラインで処理することになりました。 BIT を持って走査することにより、 $O(N\log N)$ 時間で (1a) で必要な数え上げができます。
(2a) $u\rightarrow Q_u\rightarrow v\rightarrow Q_v$ , (3a) $u\rightarrow Q_u\rightarrow Q_v\rightarrow v$
このパターン、特に (2a) では
- $u\neq Q_u$ のとき、頂点 $u$ の代わりに、 $Q_u$ に隣接する頂点のうち $u$ に最も近い頂点を使い、
- $v\neq Q_v$ のとき、頂点 $Q_v$ の代わりに、 $v$ に隣接する頂点のうち $Q_v$ に最も近い頂点を使う
ことにしても条件が表すことは変わりません。
全方位木 DP が使えます。簡単のため、 $u\neq Q_u$ かつ $v\neq Q_v$ の場合のみ考えますが、そうでない場合も、各頂点についてそれに隣接するダミー頂点を作れば同時に処理できます。
辺の向きを区別する全方位木 DP では、各辺について、「まずその辺(e)から始めることにして、同じ頂点を通らないようにして木上を移動するとき、 (e) 以外に通過できる辺(f)」の集約を計算できます。 (e) を「 $u$ から $Q_u$ までの単純パスの最後の辺」、 (f) を「 $v$ から $Q_v$ までの単純パスの最初の辺」と言い換えると、ちょうど求めたいものになります。
(3a) についても同様です。
まとめ
以上より、 $P$ の類似度が $1$ であるかどうかを $O(N\log N)$ 時間で判定するアルゴリズムが得られました。
「 $a,b,c,\ldots $ を順に含むような木上のパス」 の性質と、木上のクエリを区間クエリに変形する典型、全方位木DP の組み合わせです。
プログラム例
AtCoder Library があれば動作するプログラム

汎用部分の実装を取り除いたもの
