参考文献
はじめに
与えられた文字列の部分文字列に関する問題を suffix array や suffix tree で解くことがあると思いますが、これに関して Universal Cup の問題を通して面白いデータ構造が紹介されていたので、競技向けにまとめて紹介します。
主に資料収集、本投稿の作成において maspy さんに協力して頂きました。ありがとうございます。
表記法
本投稿では、原則 $1$ つの文字列 $s$ に対する処理を扱います。 $s$ の長さを $n$ とします。 $s$ の $i$ 文字目(最初の文字を $0$ 文字目とします)を $s_i$ で表します。 $s$ の部分文字列 $s[l,r)$ とは、 $s_ls_{l+1}\cdots s_{r-1}$ で表される文字列です。
文字列 $s$ の文字を逆順に並べた文字列 $s_{n-1}\cdots s_1s_0$ を $\mathtt{rev}(s)$ とします。
文字列の各文字は $0$ 以上 $\sigma$ 以下の整数で表されているとします。特に、 $\sigma \leq n$ を仮定します。
関連するデータ構造
Suffix Array , LCP Array
$s$ の接尾辞全体 $s[0,n) , s[1,n) , \ldots , s[n-1,n)$ を辞書順でソートしたときの順番を表す長さ $n$ の配列を suffix array といい、 $\mathtt {SA}$ で表します。つまり、 $0\leq i \leq n-2$ について辞書順で $s\left[ \mathtt{SA}[i],n \right)\lt s\left[\mathtt{SA}[i+1],n\right)$ が成り立ちます。
$s\left[ \mathtt{SA}[i],n \right)$ と $s\left[\mathtt{SA}[i+1],n\right)$ を先頭から順に比較したときに連続して一致している文字数を $\mathtt{LCP}[i]$ とおき、この長さ $n-1$ の配列 $\mathtt{LCP}$ を LCP array といいます。
suffix array および LCP array は $O(n)$ 時間で計算できます。
Suffix Tree
$s$ の接尾辞全体 $s[0,n) , s[1,n) , \ldots , s[n-1,n)$ から構築した patricia tree を suffix tree といいます。
suffix tree の説明は、 Wikipedia または他のサイト(ex. Suffix Tree + Suffix Array = Suffix Tray – Qiita @goonew)に譲ります。
suffix tree は suffix array と LCP array を用いて $O(n)$ 時間で構築できます。 $i$ の昇順に走査しながら、 $s[\mathtt{SA}[i],n)$ に至るパスの頂点を stack で管理すれば可能です。
ここで重要なクエリとして、「 $l,r$ が与えられたときに部分文字列 $s[l,r)$ を読み込んだときの suffix tree 上の位置を取得する」というものがあります。 suffix tree の heavy-light decomposition を用いて $s[l,n)$ から根までのパスを二分探索すれば $O(\log n)$ 時間で計算できます。 $O(1)$ 時間の方法もあるらしいです(*1)。
(*1) Belazzougui, Djamal, et al. “Weighted ancestors in suffix trees revisited.” arXiv preprint arXiv:2103.00462 (2021). https://arxiv.org/abs/2103.00462
Suffix Automaton
$s$ の接尾辞全体 $s[0,n) , s[1,n) , \ldots , s[n-1,n)$ を過不足なく受理する最小の DFA (決定性有限オートマトン)を suffix automaton といいます。 suffix automaton については、 Suffix Automaton – よすぽの日記 を参照するとよさそうです。
$s$ の suffix automaton のノードは $\mathtt{rev}(s)$ の suffix tree の頂点と $1$ 対 $1$ で対応します。さらに suffix automaton の failure link(*1) は $\mathtt{rev}(s)$ の suffix tree における辺に対応します。
suffix automaton は $\mathtt{rev}(s)$ の suffix tree を用いて $O(n)$ 時間で構築できます。具体的には、 $\mathtt{rev}(s)$ の suffix tree において $\mathtt{rev}(s[0,r))$ と $\mathtt{rev}(s[0,r+1))$ それぞれを表すパスを比較し、それらのノードの間に文字 $s[r]$ の遷移を追加します。このアルゴリズムの動作は、次の grid system によって図解されます。
(1) 適切な用語ではないかもしれません。 suffix automaton のノード $v$ が受理する最長の文字列を $\mathtt{str}(v)$ とするとき、開始状態以外のノード $a$ の failure link は $\mathtt{str}(a)$ の接尾辞(それ自身を除く)を受理するノード $b$ のうち $\mathtt{str}(b)$ が最長のものを指すポインタであるとします。
Grid System , Basic Substring Structure(BASS)
Grid System とは
任意の文字列に対して grid system の様子を確認できるサイトを用意しました。
$s$ の部分文字列 $s[l,r)$ 全体を、 $r$ を行、 $l$ を列に対応させて $2$ 次元グリッド状に並べることを考えます。 $s={}$abcab の場合を図に示します。
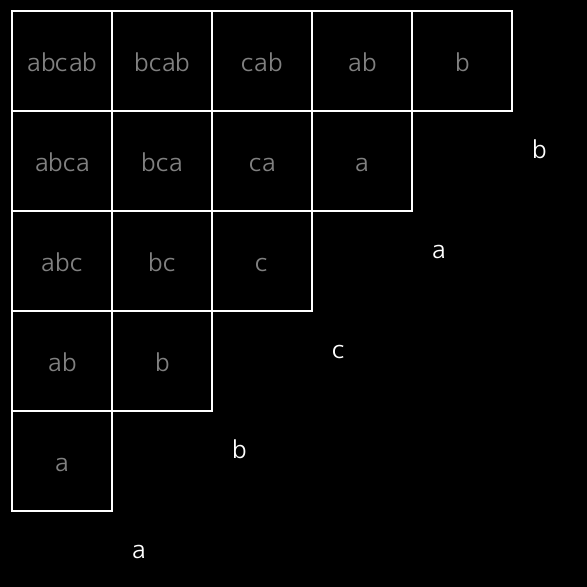
このグリッドをブロックに分割します。隣接するマスは、 $s$ 中の出現回数が等しい場合に同じブロックに含まれます。 $s={}$abcab の場合、 a , b , ab は $2$ 回ずつ出現しますが、 c を含む部分文字列は $1$ 回しか出現しません。よって、図のように、グリッドは $3$ 個の領域に分割されます。その $3$ 個がそれぞれブロックです。
このように分割したとき、各ブロックの形はヤング図形になります(*1)。特に、ブロックの境界線のうち横(縦)方向のものは必ず、右(下)方向にグリッドの端まで伸びます(*2)。
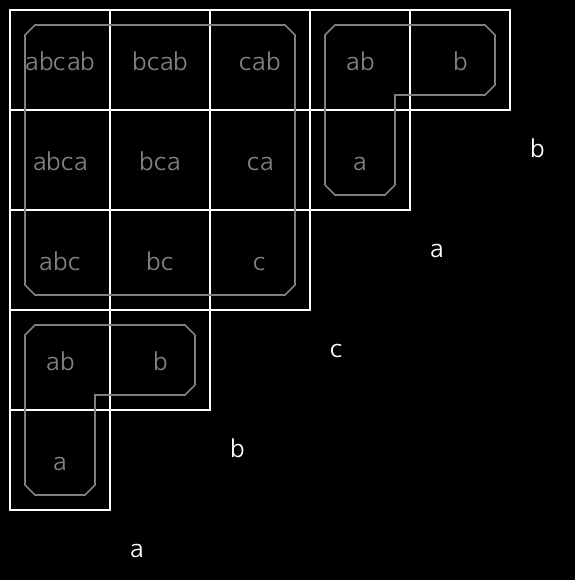
abcab には ab が $2$ 回現れるので、 a , b , ab をもつブロックは $2$ 個同じ形で現れます。このように、複数回現れる部分文字列に対応して複数回現れるブロックは、計算上は区別しません(*3)。
(*1) $\alpha$ , $\beta$ を文字、 $v$ を文字列として、 $v$ , $\alpha v$ , $v\beta$ の出現回数が等しいなら $\alpha v\beta$ の出現回数もそれに等しくなります。よってブロックが左上で凹んだ形になることはありません。
(*2) $\alpha$ を文字、 $v$ を文字列として、 $v$ と $v\alpha$ の出現回数が異なる場合、ある $\beta$ ( $\beta$ は文字または $s$ の終端を表すとする)を用いて $v\beta$ が $1$ 回以上出現します。このとき $v$ の空でない任意の接尾辞 $w$ についても $w\beta$ と $w\alpha$ が出現するので、 $w$ と $w\alpha$ の出現回数は異なります。
(*3) 論文では、 block は複数回別々に現れるものであり、同じ部分文字列に対応する block を同一視したものは equivalence class と呼ばれています。結局 $1$ つの equivalence class に対して block $1$ つ分のみのデータを持つということには変わりません。
Grid System と Suffix Tree の関係
$s$ の suffix $s[i,n)$ は、一番上の行の左から $i$ 番目( $0$-based )のマスに対応します。 suffix tree において $s[i,n)$ を読み込むときに通るパスは、グリッドでは左から $i$ 番目の列全体に対応します。このとき、
- $s$ の suffix tree の辺はブロックの列と 1 対 1 で対応し、辺のラベルの長さは列の縦の長さに等しい。
- suffix tree の辺に沿って根に近づく移動はグリッド内を下に向かって移動することに対応する。
ということが言えます。なぜなら、 suffix tree を根からたどる過程で、
- 後ろに $1$ 文字伸ばすときに分岐がある場合、 $s$ の部分文字列としての出現回数が減少するので、 grid system においてブロックが切り替わる。
- 逆に、分岐しない場合、すべての出現位置において次の文字が同じであるということなので、 $s$ の部分文字列としての出現回数は変化しない。
ということが成り立つからです。
グリッドの行と列を入れ替えることにより次のことが言えます:
$\mathtt{rev}(s)$ の suffix tree の辺はブロックの行と 1 対 1 で対応し、辺のラベルの長さは行の横の長さに等しい。 suffix tree の辺に沿った移動はグリッドを左に向かって移動することに対応する。
Grid System と Suffix Automaton の関係
以下の関係があります。
- $s$ の suffix automaton のノードは、開始状態を除いて、ブロックの行と 1 対 1 で対応する。
- suffix automaton の辺に沿った移動はグリッドを上に向かって移動することに対応する。
- suffix automaton のノード $v$ に至るまでに読み込まれる文字列としてありうるものは、 $v$ に対応する行に含まれるもの全体に一致する。
- suffix automaton の受理状態は、グリッドの一番上の行が占める部分に対応する。
- suffix automaton のノードがあるブロックにおいて最も上にある行に対応する必要十分条件は、受理状態であるまたは遷移先が $2$ 通り以上ある(出次数が $2$ 以上である)ことである。
Basic Substring Structure とその構築方法
grid system の各ブロックの形とブロック同士の位置関係を計算して得られるデータ構造を basic substring sutructure (BASS) といいます。例えば、各ブロックについて以下の情報を計算します。
- 各行について、
- 長さ(=マスの個数)
- その右にある(他のブロックの)行へのポインタ
- 最も左のマスの $1$ つ下のマスが属する行へのポインタ
- 各列についても同様
- ブロックに属する最長の部分文字列の長さ
BASS は $s$ の suffix tree と suffix automaton 、および $\mathtt{rev}(s)$ の suffix tree と suffix automaton を一度に表現します。 BASS を構築するときにはまずそれらを構築することになります。
例えば次の手順で BASS を構築できます。
- $s$ の suffix automaton と $\mathtt{rev}(s)$ の suffix tree を計算する。(開始状態あるいは根を除いた各ノードは、 BASS においてあるブロックの行に対応する。)
- suffix automaton のノードを、受理される文字列(*1)の最大長の長い順に見る。受理状態でなく出次数が $1$ であるノードは、そのただ $1$ つの辺の先にあるノードと同じブロックに対応する。
- ブロックを構築する。行の長さは $\mathtt{rev}(s)$ の suffix tree においてラベルの長さに一致する。
- ブロック内の各行についての右方向のリンクを、 $\mathtt{rev}(s)$ の suffix tree から得る。
- ブロック内の各行についての下方向のリンクを、 $s$ の suffix automaton から得る。
ブロックの行の総数も列の総数も $O(n)$ であるため、ブロックの各行や各列に関する前計算ができます。
(*1) 開始状態からそのノードに至るまでに読み込む文字列としてあり得るもの
Internal Dictionary Matching (IDM) Problem
$0,1,\ldots ,m-1$ について $l_i ,r_i$ が与えられるので、それぞれ $d_i=s[l_i,r_i)$ とします。以下の $2$ 種類のクエリを考えます。
- $\mathrm{Count}(l,r)$ : $s[l,r)$ の部分文字列として $d_i$ が現れる回数を $k_i$ とするとき、 $\sum_i k_i$ の値を求める。
- $\mathrm{CountDistinct}(l,r)$ : $s[l,r)$ の部分文字列として $d_i$ が $1$ 回以上現れるような $i$ の個数を求める。
Count クエリを解く
basic substring structure を用いれば $\mathrm{Count}$ クエリが Rectangle Sum に帰着します。 Rectangle Sum は、例えば wavelet matrix を用いてクエリあたり $O(\log n)$ 時間で処理できます。
まずグリッドを用いて言い換えると、 $d_i$ はそれぞれブロック内部のあるマスに印をつける(ただし、ブロックが複数回現れる場合は、すべての出現位置に対して印をつける)ことに対応し、 $\mathrm{Count}(l,r)$ の値は、ある長方形領域に含まれる印の個数に等しくなります。
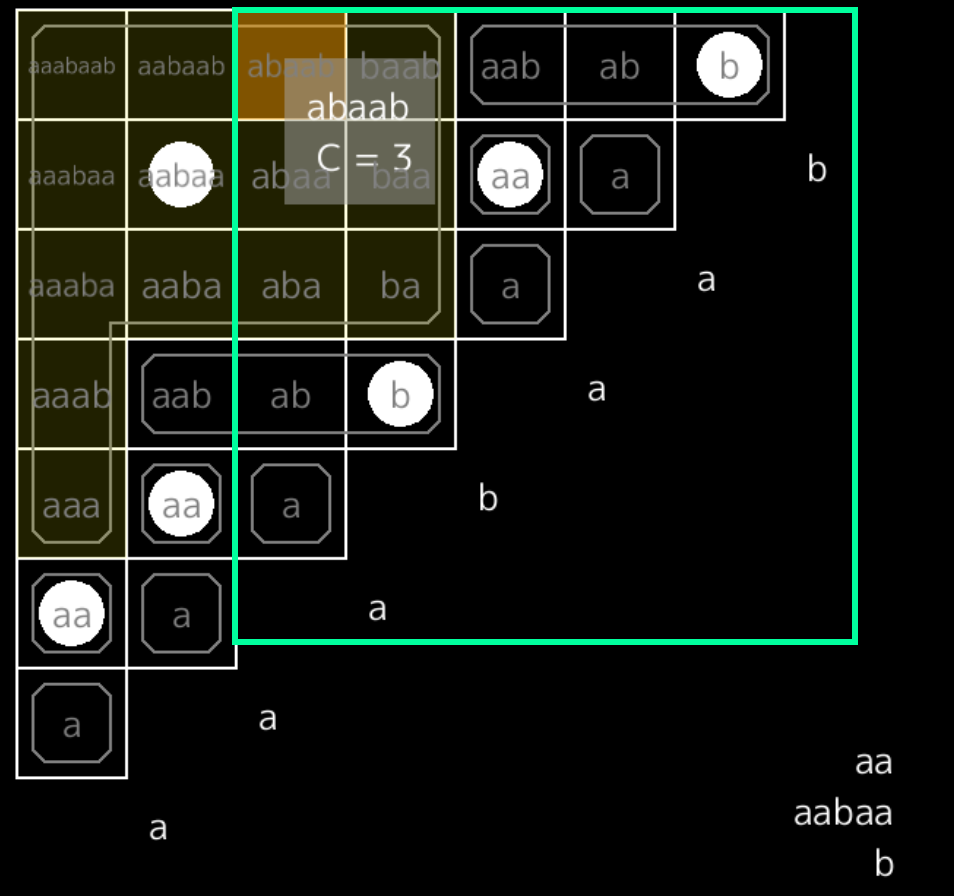
$s[2,7)=\mathtt{abaab}$ には $d_0$ が $1$ 回、 $d_1$ が $0$ 回、 $d_2$ が $2$ 回現われるので、$\mathrm{Count}(2,7)$ の値は $3$ です。
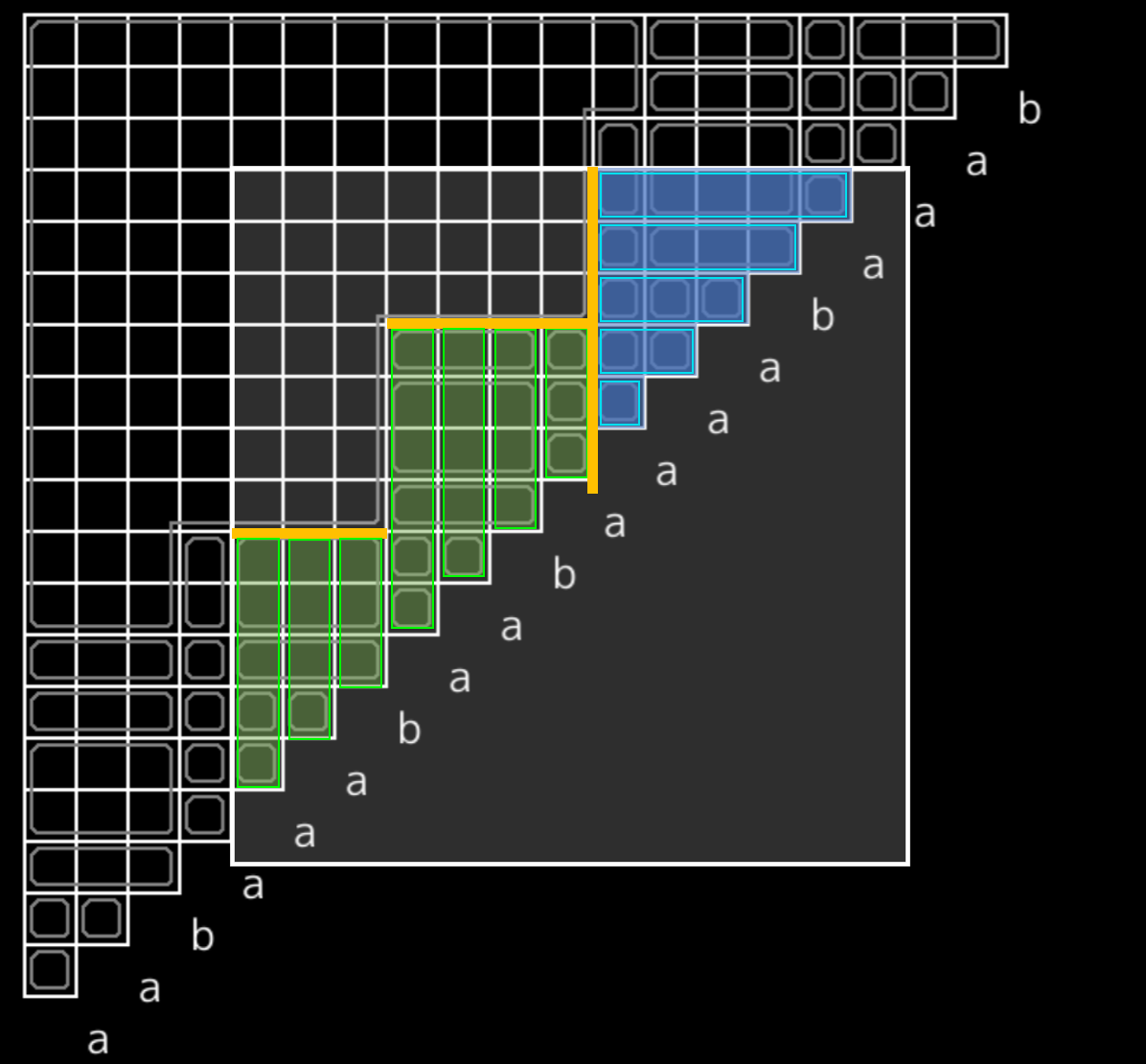
長方形領域を分割します。下図の図中では、ある $\mathrm{Count}$ クエリに対応する長方形領域を半透明の白で塗っています。
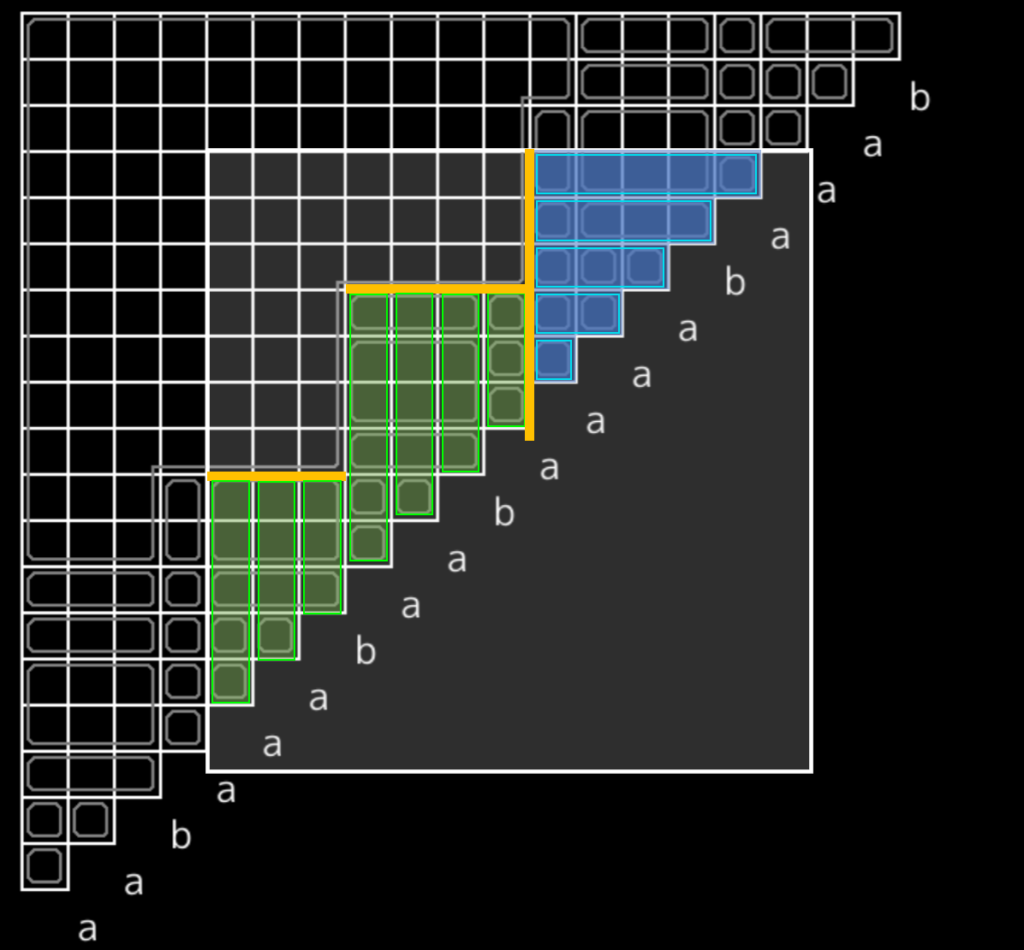
- まず、最も左上のマスが属するブロックを見つけます。 suffix tree 上の $s[l,n)$ から根までのパスについて二分探索します。例えば heavy-light decomposition を用いて $O(\log n)$ 時間で求まります。
- 最も左上のマスが属するブロックについては、単に Rectangle Sum を解けばよいです。
- 下側の領域(図中緑色)は、ブロックの列ごとに印の個数を計算し、下から上へ累積和をとり、さらに各ブロックの下端に沿って累積和をとるということを事前に行えば十分です。
- 右側の部分(図中青色)は、ブロックの行ごとに印の個数を計算し、右から左へ累積和をとり、さらに下から上へ累積和をとるということを事前に行えば十分です。
以上により、 $\mathrm{Count}(l,r)$ の値は $O(\log n)$ 時間で計算できます。
IDM の CountDistinct の解法
ある木クエリ
根付き木があり、各頂点には $0$ で初期化されたラベルがついています。以下のクエリを処理してください。
$\mathrm{Update}(s,b)$ : 頂点 $s$ から根 $\mathtt{root}$ までの単純パス上の頂点のラベルを順に並べた列の連長圧縮表現(*1)を求めてください。その後、頂点 $s$ から根 $\mathtt{root}$ までの単純パス上のすべての頂点のラベルを $b$ に置き換えてください。
連長圧縮表現について、より具体的には、以下の条件を満たす $3$ つ組 $(u_i,v_i,a_i)$ の列を出力してください。
- $0\leq i \lt k$ について、 $v_i$ は $u_i$ の祖先( $u_i=v_i$ も OK )であり、 $u_i$-$v_i$ 間のパス上の頂点のラベルは $a_i$ である。
- $0\leq i\lt k-1$ について、 $u_{i+1}$ は $v_i$ の親である。
- $u_0=s$ , $v_{k-1}=\mathtt{root}$ 。
splay tree を用いた link-cut tree の実装を用いればすぐに解法が得られます。つまり、クエリごとに $s$ を expose して、訪れた solid path ごとに $(u_i,v_i,a_i)$ を取得すれば答えられます。 expose の時間計算量が償却 $O(\log n)$ であるように、このクエリの計算量と出力長は償却 $O(\log n)$ です。
ここでは link-cut tree を用いることにしましたが、木の形は変化しないので heavy light decomposition でも高速に処理できます。詳細は、 JOI の問題「高速道路の建設」を参考にしてください。
以降では、 CountDistinct のための前計算として、 $s$ と $\mathtt{rev}(s)$ それぞれの suffix tree においてこのクエリを処理します。ただし、このとき $v_i$ を取得する必要はありません。
(*1) ランレングス圧縮。 run length encoding.
最小のユニークな接尾辞の発見
問題:
$\mathtt{pos}_{l,r}$ を、部分文字列 $s[l,r)$ 内の $s[p,r)$ の出現回数が $1$ であるような $p$ の最大値とします。 $O(n\log n)$ 時間の前計算のもと、一つの $(l,r)$ に対して $O(\log n)$ 時間で $\mathtt{pos}_{l,r}$ を求めてください。
$\mathtt{rev}(s)$ の suffix から生成した trie を考え、 $r$ を $1$ から $n$ まで動かし、 $\mathtt{rev}(s[l,r))$ として現れる頂点にラベルを $r$ で上書きするという手順を考えます。上書きする直前のラベルの値は、その頂点が示す部分文字列の直前の出現位置なので、これを用いて $\mathtt{pos}_{l,r}$ を計算できます。
上書き直前のラベルの値の連長圧縮表現は先に述べた木クエリを $\mathtt{rev}(s)$ の suffix tree 上で行えば、すべての $r$ について $O(n\log n)$ 時間で得られます。 $\mathtt{pos}_{l,r}$ を計算するときは、この連長圧縮された列を二分探索すれば、 $O(\log n)$ 時間で値を得られます。図中にある $r-\mathtt{pos}_{l,r}$ のグラフ概形を参照してください。
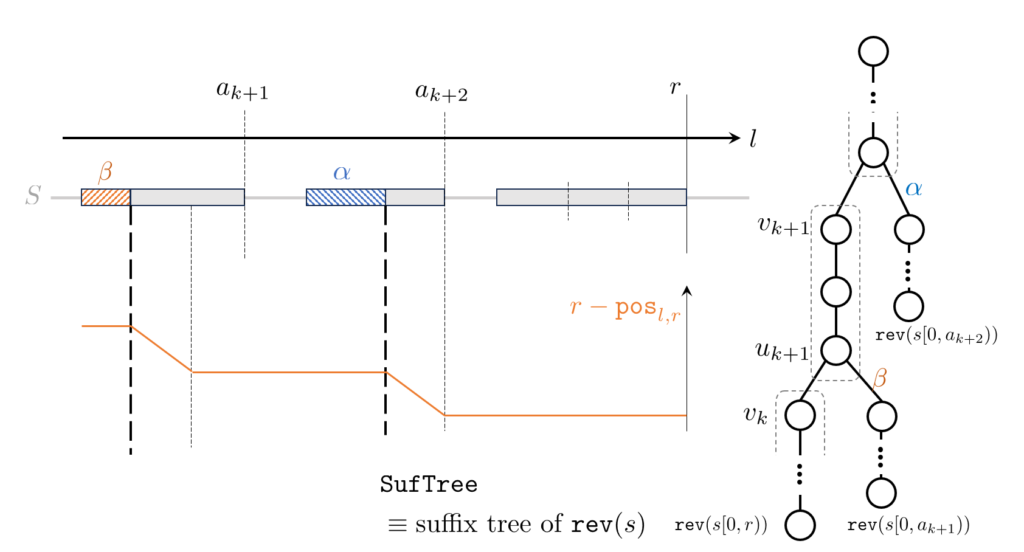
図の状況における例として、例えば $l$ が $2$ つの太い破線の間に位置するようなクエリに対しては、その $2$ つの太い破線の間の橙実線をなす $2$ つの線分を考慮すればよいです。よって、 $a_{k+1},a_{k+2}$ の値と、 $u_{k+1},u_{k+2}$ それぞれに対応する文字列の長さの情報から $\mathtt{pos}_{l,r}$ の値が得られます。
CountDistinct の解法
$s[l,r)$ の suffix から生成した trie に含まれる頂点全体は、 $s[l,r)$ の部分文字列全体に対応します。この trie は $s$ の suffix から生成した trie の部分グラフであり、 CountDistinct の答えはこの部分グラフの頂点全体の重みの総和で表せます。(頂点の重みは、辞書に含まれる文字列のうち、その頂点に対応する文字列に一致するものの個数とします。)
$\mathrm{Count}(l,r)$ の値は、 $k=l,l+1,\ldots ,r$ について $s[k,r)$ に対応する頂点から根までのパス上の頂点の重みの総和を足し合わせたものになるので、ここから重複分を以下のように除くことで $\mathrm{CountDistinct}(l,r)$ の値を得ます。
- $s[k,r)$ が他のパスに含まれている場合。これはちょうど $\mathtt{pos}_{l,r}+1\leq k$ の場合なので、まとめて $\mathrm{Count}(\mathtt{pos}_{l,r}+1,r)$ で重複分を得られます。
- $s[k,r)$ が他のパスに含まれない場合。重複は trie の分岐点から始まるので、分岐点ごとに寄与を考えます。この重複分全体の重みを $D[l,r)$ とおきます。(*1)
すなわち次の式が成り立ちます。
$$\mathrm{CountDistinct}(l,r)=\mathrm{Count}(l,r)-\mathrm{Count}(\mathtt{pos}_{l,r}+1,r)-D[l,r)$$
図のように、各頂点について、根からその頂点までのパス上の重み和を計算しておけば、重複分はすべて trie の分岐点にかかります。以降は trie の分岐点のみ考えるので、分岐しない部分を圧縮したものである suffix tree で管理すれば十分です。
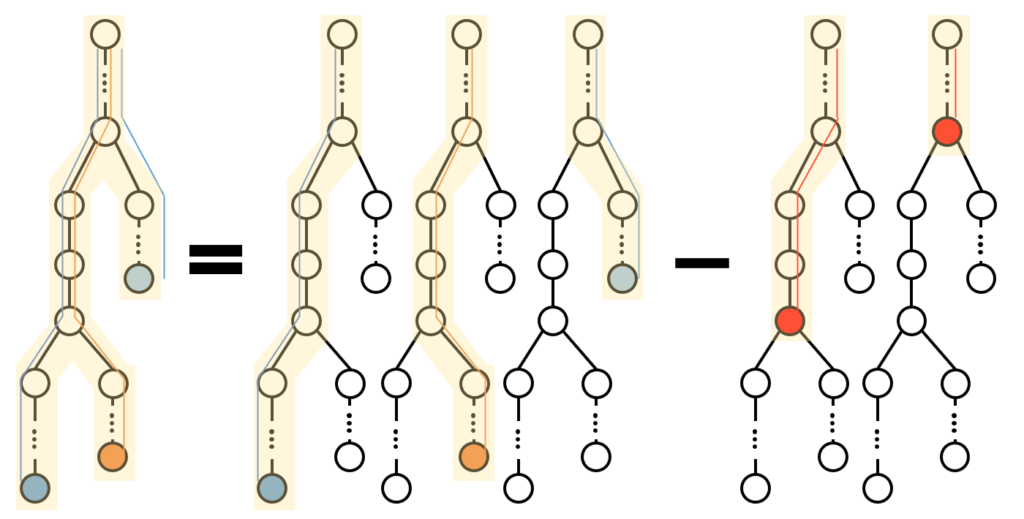
trie 内に分岐点 $v$ の子が $k$ 個含まれるとすると、 $2\leq k$ のときに限り分岐点の重みの $k-1$ 倍を重複分として引かなければなりません。
$l$ を固定したときのすべての $r$ についての $D[l,r)$ の値を並べた配列を考えます。 $l$ を $1$ だけ減らすとどのように変化するでしょうか。 $s[l,r)$ から根までのパスを新たに考慮することになりますが、このパスと他のパスが $t=s[l,p)$ に対応する頂点で新たな分岐をなす条件は
- 他のパスが $s[l,p+1)$ を含まない
- 他のパスが $s[l,p)$ の子を $1$ つ以上含む
の両方を満たすことです。 $s[p]=\alpha$ , $s[l,p+1)=t\alpha$ として言い換えると、「 $s[l+1,r)$ に $t\alpha$ は現れないが、ある $\beta\neq \alpha$ について $t\beta$ が現れる」ということです。よって、 $l$ 文字目よりも後ろの $t$ の最初の出現位置と $t\alpha$ の最初の出現位置から、条件を満たす $r$ の範囲を下図のように求められます。そしてこの「 $l$ 文字目よりも後ろの~の最初の出現位置」は $\mathtt{pos}$ の求値のときと同様に suffix tree 上の木クエリですべて計算できます。
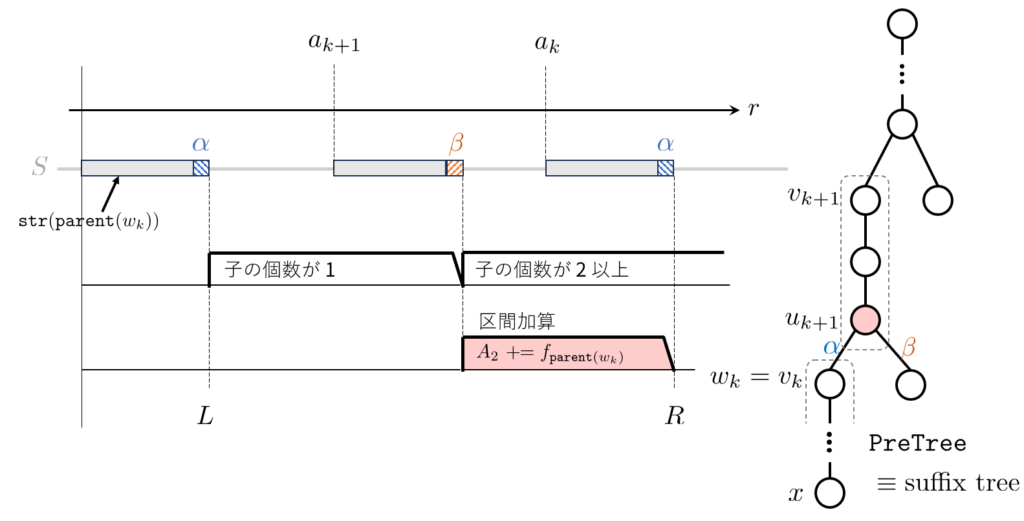
したがって、すべての $r$ についての $D[l,r)$ の値を並べた配列について、 $l$ を $1$ だけ減少させたときの変化を区間加算で表すことができ、また $l$ を $n$ から $0$ まで変化させたときの区間加算の回数の合計は $O(n\log n)$ になります。オフラインクエリの場合は binary indexed tree で走査し、オンラインクエリの場合は永続セグメント木を用いれば、どちらも前計算 $O(n(\log n)^2)$ 時間+クエリ $O(\log n)$ 時間で重複分 $D[l,r)$ を計算できます。
以上により、 $O(n(\log n)^2)$ 時間の前計算の後 $\mathrm{CountDistinct}(l,r)$ を $O(\log n)$ 時間で計算できます。
(*1) 論文では $A_2$ と表されています。本投稿では $l,r$ を変化させる状況を分かりやすくするために $D[l,r)$ と表します。