参考文献
[1] Alon, Noga. “A simple algorithm for edge-coloring bipartite multigraphs” (https://www.tau.ac.il/~nogaa/PDFS/lex2.pdf)競プロライブラリ用はこの方法がよくて、また短くて簡単なのでさっと読めます。
[2] Cole, Richard, Kirstin Ost, and Stefan Schirra. “Edge-coloring bipartite multigraphs in O(E logD) time.” (https://cs.nyu.edu/media/publications/TR1999-792.pdf)最強計算量
[3] Schrijver, Alexander. “Bipartite edge coloring in O(Δm) time.” (https://homepages.cwi.nl/~lex/files/edgecol.pdf) [4] Kapoor, Ajai, and Romeo Rizzi. “Edge-coloring bipartite graphs.” (https://romeorizzi.github.io/papers/pdf/ajai.pdf) [5] Cole, Richard, and John Hopcroft. “On edge coloring bipartite graphs.” (https://ecommons.cornell.edu/server/api/core/bitstreams/964662f6-3f78-4acf-9ac0-b69c0b478e97/content)問題
グラフの $k$-辺彩色とは、各辺に $k$ 色のうち $1$ 色を割り当てて、端点を $1$ つ以上共有するようなどの $2$ 辺の色も異なるようにすることです。
$N$ 頂点 $M$ 辺、最大次数 $D$ の、単純とは限らない二部グラフがあります。実は(*1)どの場合でも $D$-辺彩色が可能なので、 $D$-辺彩色を $1$ つ求めてください。
この概念自体は AtCoder の出題例にも当てはまることが あり ます。
(*1) 以降で示す方法で $D$-正則二部グラフに変換すると、ホールの定理より完全マッチングが存在します。繰り返せば、 $D$-辺彩色になります。
単純化
以下の手順で、(辺の本数を $O(M)$ に保ちつつ)すべての頂点の次数が $D$ になります。このようなグラフを $D$-正則二部グラフといいます。
- 左側頂点と右側頂点に分けます。(Library Checker の問題ではすでに分けられています)
- 次数 $D$ 以下を保ちつつ、片側の頂点数が $O(M/D)$ になるように頂点を合体します。
- 頂点と辺を適切に追加します。
以降では $M=ND/2$ が成り立つものとして、計算量は比較のために $N$ , $D$ で表します。
Library Checker のテストケースについて少し
アルゴリズムは二部グラフの完全マッチングを利用します。よって二部グラフのマッチング問題向けのテストケースを追加するときは Edge Coloring of Bipartite Graph への追加も検討したいです。
Euler splitting
奇数次の頂点の個数を $2p$ とすると、グラフの辺集合は
- $0$ 個以上のサイクル
- $p$ 個の単純パス
に分割できます。具体的にはサイクルを貪欲に取り除けばよいです。
特に、 $2n$-正則二部グラフはすべて偶数長のサイクルに分割されます。各サイクルの辺を交互に振り分ければ、 $2$ 個の $n$-正則二部グラフが得られます。計算量は $O(M)$ つまり $O(ND)$ です。
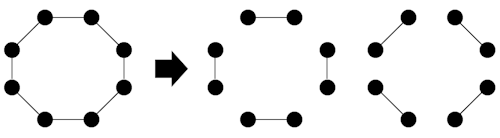
再帰的な Euler splitting により、 $D=2^d$ ( $d$ は整数)であれば $D$-辺彩色が $O(ND\log D)$ 時間で得られます。
[2] によると、ここでのサイクル・パスへの分割を Euler partition 、それによってグラフを $2$ つに分割することを Euler splitting といいます。
辺彩色アルゴリズム
$D=1$ の場合は自明です。 $2\leq D$ のとき、 $D$ の偶奇で場合分けします。
- $D=2d+1$ の場合、完全マッチングを $1$ つ求め、偶数の場合に帰着します。
- $D=2d$ の場合、 Euler splitting で $d$-正則二部グラフ $G_2$ , $G_3$ を得て、 $G_2$ を $d$-辺彩色します(再帰)。 $G_3$ 全体と $G_2$ の一部から $2^n$-正則二部グラフを作れば、これは $O(ND\log D)$ 時間で彩色できます。
完全マッチングの計算を除けば $O(ND\log D)$ 時間です。
少しだけ最適化できます。後半で $2^n$ で揃える代わりに、奇数が出て来しだい $1$ 色だけ借りて分割すれば十分です。
マッチング回数の最適化
マッチングアルゴリズムの選択によっては、ここは不要です。
さっきの方法では分割過程で奇数の次数が現れるごとにマッチングをとることになりますが、実は最初の $1$ 回だけマッチングをとれば後は Euler splitting で $O(ND\log D)$ 時間のアルゴリズムが成立するということが [4] で示されています。
次数を完璧に半分にしなくても、半分以下のサイズのピースに分割できていれば全体のアルゴリズムが成立することに注意します。はじめ、マッチングと Euler splitting によって、正則二部グラフの次数が $(2d+1)$ から $1,d,d$ に分割されます。このような $3$ つの正則二部グラフ(次数 $a,b,b$ )に対して、偶奇で場合分けして
- (奇,偶,偶) のとき $a,\frac{b}{2},\frac{b}{2},b$ に更新して $b$ を捨てる
- (奇,奇,奇) かつ $a\neq b$ のとき $b, \frac{a+b}{2} , \frac{a+b}{2}$ に更新する
とすれば、必要な条件( $a$ が奇数 , ($a\neq b$ または $a=b=1$) , $\gcd (a,b)=1$ )を保ったまま分割が進みます。
D-正則二部グラフの完全マッチング
一般の二部グラフと同様に Hopcroft–Karp アルゴリズムを用いると $O(M\sqrt{N})$ つまり $O(ND\sqrt{N})$ 時間ですが、正則二部グラフに対してはもっと高速な方法があります。
A : O(ND log N) 時間
[1] で示された方法です。 Library Checker での私(Nachia)の提出 #228343 は、これを工夫して実装したものです。辺の多重度を $\alpha$ 倍し、さらに多重度 $\beta$ で完全マッチングをなす辺(ゴミ)を追加します。 $M\leq 2^m = D\alpha +\beta$ かつ $0\leq \beta\lt D$ となるように $\alpha,\beta$ をとれば $2^m$-正則グラフが得られるので、 Euler splitting を $m$ ($=\lceil \log_2 M\rceil$) 回繰り返せます。ゴミの辺は $2^m$ 個よりも少ないので、分割のたびにゴミが少ないほうを選んで残せば、最終的にゴミが $0$ 個の完全マッチングが得られます。
$2^m$-正則グラフは直接管理できませんが、「多重度 $2^a$ の辺は $a$ 回分割後に多重度 $1$ として追加」とすればよいため、 $\alpha$ および $\beta$ を $2$ 進法で表して適切なタイミングで追加すれば、追加する辺の個数は全部で $O(ND\log N)$ です。追加する各辺が計算量に $O(1)$ で寄与するので、完全マッチングは $O(ND\log N)$ 時間で得られます。
$D$-辺彩色の計算量は $O(ND(\log N + \log D))$ すなわち $O(ND\log (ND))$ です。
ゴミは実際に追加せず implicit に処理できます。 Euler splitting の計算で奇数次の頂点で行き止まりになった後は、なるべくその相方の頂点からスタートすることにしさえすればよいです。
[5] Algorithm 1 が似たアルゴリズムです。部分グラフの偶数次の頂点が増加するように Euler splitting とマージを繰り返して偶数次の正則二部部分グラフを得、さらに Euler splitting をすると、考えるべき辺の本数が半分以下になる、というものです。戦略は下図のようにします。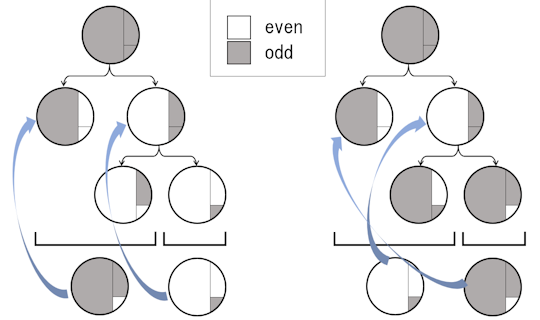
実は、図中の右のパターンは、ゴミを利用する方法において、「与えられた $D$-正則グラフを追加して Euler splitting する」という操作に対応します。これにより、辺を追加する処理に関して、与えられたものよりも多くの多重辺を作らずに処理できます。
B : O(ND^2) 時間
[3] で示された方法です。 [1][5] とは異なるアプローチで、これの高速化が [2] です。$D$-正則二部グラフという条件を保って辺の多重度を変化させます。
$2L$ 辺の単純サイクルを見つけたとします。例えば偶数番目の辺の多重度を $+1$ 、奇数番目の辺の多重度を $-1$ するという操作は、頂点の次数を変化させません。これを繰り返すと、すべての辺の多重度が $0$ または $D$ となり、完全マッチングが得られます。
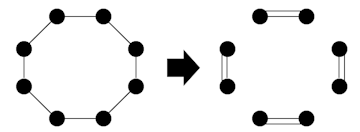
偶数番目と奇数番目のうち辺の多重度の合計が大きいほうを $+1$ 、もう一方を $-1$ します。多重度が $0$ になった辺は削除します。サイクルの検出を DFS でやると、長さ $2L$ のサイクルを発見するごとに $O(L)$ 時間で処理できます。多重度 $x$ の辺に対して $x^2$ の重みをつけると、この操作で重みが $2L$ 以上増加し、この重みは最大 $ND^2$ であるため、計算量は $O(ND^2)$ になります。
C : O(ND) 時間
いよいよ、現状最良計算量(*1)の [2] の方法です。
C’ : 辺の削減
多重度 $1$ の辺のみに対してサイクルを貪欲に取り除けば、多重度 $1$ のサイクルを持たないグラフと多重度 $2$ のグラフに分けられます。これを繰り返すと、多重度 $1$ , $2$ , $4$, $\ldots$ , $2^{\lfloor \log D\rfloor}$ の、それぞれサイクルを持たないグラフが残り、すなわち相異なる辺の個数は $O(N\log D)$ になります。各階層で辺の数が半分になるので、この部分の計算量は $O(ND)$ です。
この処理の後にアルゴリズム A を行う (C’A) と、マッチングの計算量が $O(N\log N\log D)$ 、全体の計算量が $O(ND \log D+N\log N \log D)$ になります。 [5] Algorithm 1 にこれを適用したものが [5] Algorithm 2 です。
スケーリングアルゴリズムの雰囲気があって、なんか良いですね
DFS
B で実行される DFS を平衡二分探索木で高速化します(*2)。探索を進める間、 $D^2$ (*3) 頂点ごとに平衡二分探索木でまとめて chain とします。多重度の最大値最小値、一様加算、総和を管理すれば、 $2L$ 辺のサイクルは $O(L\log D/D^2)$ 時間で処理できます。多重度 $0$ の辺を削除した後、サイクルの部分に残った chain はそのままにしておきます。
進みたい頂点が chain に含まれる場合、その分一度に進みます。 chain の中間にある頂点に進む場合は、長く進める方に進みます。 chain を構築するぶんの計算量は、すべてポテンシャルに押し付けます。具体的には、
- chain に含まれない辺の重みを $\log_2 (D^2)$
- 探索中のパスに含まれる chain の重みを $0$
- 探索中のパスに含まれない $t$ 辺 ( $t\geq 2$ )からなる chain の重みを $\log_2 (D^2)\log_2 t$ (*4)
とします。
また、サイクル発見時にそのサイクルに含まれる高々定数個の chain の長さが $D^2$ 未満になりますが、これは辺の本数を $O(N\log D)$ としたことによりサイクル発見回数が抑えられ、計算量への寄与は $O(N(\log D)^3)$ になります。
$O(ND)$ 時間で正則二部グラフの完全マッチングが得られるので、 $D$-辺彩色は $O(ND\log D)$ 時間です。
(*1) 辺彩色をこれよりも速くしようとすると、 Euler splitting による再帰的分割を脱さないといけません。
(*2) 定数倍やばそう
(*3) [1] ではこのパラメータを $s$ とおいて議論を進め、全体の計算量を決める段階で $s=D^2$ と選んでいます。
(*4) これにより、 chain 分割時に長いほうを消費すれば $\log_2 (D^2)$ の計算量を償却できます
おわり