競技プログラミングの話題です。
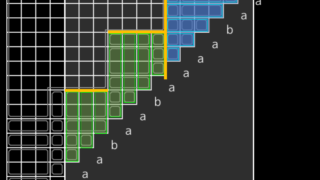
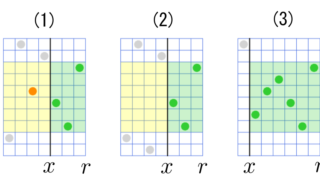
競プロ 部分文字列の編集距離の Monge 性（仮公開）
まとまった内容ではありませんが、（コンテスト問題に対して解法解説とかをやらなくなったものあって）記事投稿頻度が減ったぶんの埋め合わせにしようと思います。
動機
（私の作問でも私の投稿でもありません）
問題概要...
アルゴリズム資料 Basic Substring Structure 解説
参考文献
はじめに
与えられた文字列の部分文字列に関する問題を suffix array や suffix tree で解くことがあると思いますが、これに関して Universal Cup の問題を通して面白い...
アルゴリズム資料 Permutation Tree (こどふぉブログ勉強月間2)
こどふぉブログ勉強月間では、 codeforces blog の積読を消化して、ついでに日本語の資料を作っておくことを目標にします。
参考資料
Tutorial on Permutation Tree (析合树）codefo...
アルゴリズム資料 対称群の部分群の簡単化(こどふぉブログ勉強月間1)
こどふぉブログ勉強月間では、 codeforces blog の積読を消化して、ついでに日本語の資料を作っておくことを目標にします。
参考資料
Permutation group basis construction (Sc...
競プロ 競プロ作問 Isekai 解説
問題概要
$H\times W$ マス目のうち、 $N$ 点は黒です。各クエリではグリッドのマス $(X,A)$ が指定されるので、
指定されたマスから左右上方向に伸ばして得られる長方形であって、
黒マスを含まず、
...
競プロ キーエンスプロコン2024（ABC374） 全問 1ms (C++)
-
競プロ AtCoder 七段 , Codeforces LGMに到達しました やったね
記念スクショ
色：#7878DB
殿堂入りページにアイコンが載るので、 AtCoder 用にアイコンを作りたいです。誰か描いて～～～
統計
AtCoder Problems Achievement
...
競プロ Library Checker 解説 永続queue (Persistent Queue)
体系的な解説はほとんどできていないと思います。それでもよければ
永続 queue とは
これのことです↓
永続 stack
前提知識です。 pop back した後の stack へのポインタを管理すれ...
競プロ Library Checker 解説 Edge Coloring of Bipartite Graph
参考文献
Alon, Noga. "A simple algorithm for edge-coloring bipartite multigraphs" (
競プロライブラリ用はこの方法がよくて、また短くて簡単なの...
レポート Euclidean MST (Library Checker) correct.cpp の解説
背景
競プロでは、ユークリッド距離最小全域木の計算方法として、 Fortune のアルゴリズムでドロネー図(Delaunay diagram)を構築し、ドロネー図の最小全域木を計算するという方法がよくとられていま...