Double-Ended Palindromic Trees 解説

Library Checker への提案を踏まえ、 [1] で提案された Double-Ended Palindromic Trees の原理をさらい、これを実際のプログラムとして実装する過程を解説します。

回文木・ stack 回文木

回文木および stack 回文木は [2] で説明されています。

回文木

文字列 $s$ に対して、回文木は $s$ の部分文字列に現れる異なる回文をノードとするもので、各ノード $v$ は

• 両側を文字 $c$ で伸ばして得られる回文 $\mathrm{next}(v,c)$
• 接尾辞の回文であって最長のもの $\mathrm{link}(v)$

へのリンクを持ちます。境界として $2$ つの特殊なノード $\mathrm{even}$ , $\mathrm{odd}$ を持ち、それぞれ長さ $0$ 、長さ $-1$ に対応します。 $\mathrm{link}(\mathrm{even})=\mathrm{link}(\mathrm{odd})=\mathrm{odd}$ とすることで、 $\mathrm{link}$ による構造が根付き木をなします。長さ $n$ の文字列に現れる異なる回文は高々 $n$ 個です。特に、末尾に $1$ 文字追加したときに新しく現れる回文は高々 $1$ 個（接尾辞である回文のうち最長のもの）です。

与えられた $s$ に対して回文木を構築するのは結構簡単^(*1)で、また Manacher のアルゴリズムも参考にすればさらにシンプルに見えると思います。

stack 化と quick link

ここで文字列を stack にする（末尾追加・末尾削除の操作を許す）と、 $\mathrm{link}$ をたどる分の計算量の償却が破綻します。しかし実は本質的な遷移先はノードごとに $O(\min (\log |s|,\sigma ))$ 個しかない^(*2) ためこれを列挙できれば償却不要となって stack の操作でも高速になります。方法としては、新しいリンク $\mathrm{quickLink}$ を次で定義して管理します：

• $s$ 中で $\mathrm{link}(v)$ の手前の文字を $c$ とする。 $\mathrm{link}$ をたどった先を $w$ として、 $w$ の手前の文字が $c$ でなくなったとき $\mathrm{quickLink}(v)=w$ とする。なければ $-1$ 。

これは新しいノードを作るごとに $O(1)$ 時間で計算でき、 $\mathrm{quickLink}$ の更新はそのノードが消えるまで起きません。これで push_back が最悪 $O(\log |s|)$ 時間になります。

(*1) 構築方法の参考： math314のブログ「Palindromic Tree」
(*2) 登場する文字列がすべて回文であることに注意すると、 KMPのK と同じ議論ができます。

deque 回文木 (Surface Recording)

本投稿では surface recording method に注目します。 occurrence recording method は解説しません。

surface recording では、 deque-回文木を実現する鍵は “surface” と “cnt” です。([1] Table 3)

surface

$s$ の回文部分文字列の取り出し方 $t$ が surface であるとは、 $t$ と左端または右端の位置が一致する回文部分文字列であって $t$ よりも長いものが存在しないことを言います。

push_back で $s$ を延長するとき、「 $s$ の接尾辞かつ回文となるもののうち最長のもの」が必要となります。これを得るために「 $s$ の各接頭辞についてそれを求めておく」ということを考えたくなりますが、それでは更新処理が間に合いません。

管理対象を surface に限定すれば、定義が双方向で対称であるため左端と右端の対応関係が必ず取れ、結果的に

• 両端では必要なデータが常に管理されている (Lemma 5.9)
• deque の操作で発生する更新の個数が $O(1)$ (Lemma 5.10, Lemma 5.12)(操作はシンプルだが、証明は地道で辛い)

となって非常に都合がよいです。

結局、 surface の左端を表す presurf と右端を表す sufsurf を管理します。ただし、その地点に surface が存在しない場合は $\mathrm{even}$ を入れます。

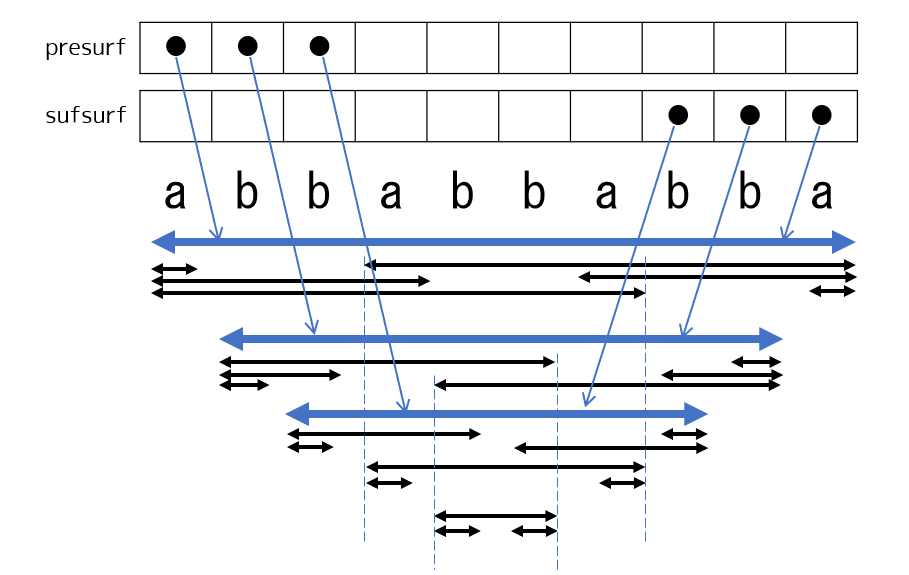
cnt

$\mathrm{cnt}(v)$ とは、 $s$ の接尾辞すべてについて最長の接頭辞回文を求めて並べたとき、 $v$ に対応する文字列が現れる回数です。実は「接尾辞」↔「接頭辞」を入れ替えても同じ値となります([1] Lemma 5.1)^(説明)。都合のよいほうに着目すれば、 deque の操作で発生する更新がほぼ自明です([1] Lemma 5.7)。

deque

そもそも deque の構造がなければ実現できません。ランダムアクセス可能な最悪定数時間の deque は幻想なのでは？というのがどのように解決されているのか把握しかねましたが、競プロではまず問題にならないでしょうし、永続化の際はいずれ永続 BBST で管理するので大丈夫というわけで、とりあえず計算量を償却するとして先に進みます。

Algorithm 9-12 での surface の更新、またサブルーチンとして必要な link の計算の際にかなり柔軟に deque にアクセスするため、例えば双方向連結リストでの実装ですべて処理するのは困難に見えました。

その他

• $\mathrm{linkcnt}(v)$ : $\mathrm{link}(w)=v$ であるような $w$ の個数です。これと $\mathrm{cnt}(v)$ から、ノードを消すタイミングを判定できます。
• $\mathrm{parent}(v)$ : $v$ の両端から $1$ 文字ずつ縮めた回文のノードです。論文では言及されていませんが、ノードを消すときの $\mathrm{next}$ の抹消のために追加しました。

deque 回文木の実装

以上で説明したデータを管理すれば、 [1] で示される疑似コード Algorithm 9-12 をもとに実装することができます（それを読みに行ってください）。ただし、特に次のことに注意します。

• 回文木本体の更新手順と linkcnt の更新は省略されています。また今回の実装では parent の更新処理を足します。
• $\mathrm{quickLink}$ の更新手順は [2] Lemma 3.1 で説明されていますが、おそらく $\mathrm{link}(\mathrm{link}(v))\neq\mathrm{odd}$ と、文字を追加する処理が完了していることを仮定しないと配列外参照があります。^(*3)
• pop に含まれる分岐の条件に $\mathrm{len} (v)\geq 2$ を追加します。^(*1)(*3)

今回はデータ構造は以下のようにして実装しました。 AmortizedDeque は std::vector を $2$ 個用いて実装した償却定数時間の deque ^(*2)です。

using Char = int; // 文字
struct Node {
    Node* parent;
    Node* link;
    Node* quick;
    std::map<Char, struct Node*> next;
    int len;
    int cnt;
    int linkcnt;
};
struct DequeNode {
    Char ch; // これで生文字列を管理
    Node* presurf;
    Node* sufsurf;
};

struct PalindromicTree {
private:
    AmortizedDeque<DequeNode> deq;
    std::unique_ptr<Node> Odd;
    std::unique_ptr<Node> Even;

// ...

全体の実装 : (GitHub Gist) https://gist.github.com/NachiaVivias/6ccf981deb58a53497bffd28b45acf88

(*1) [1] Lemma 5.12 の証明で条件が明示されています。確かに他の条件から導かれますが、プログラムにすると配列外参照になってしまいます。
(*2) 参考： slideshare 「Amortize analysis of Deque with 2 Stack」Ken Ogura より
(*3) このへんの配列外参照は「長さ $9$ 以下の 012-文字列、あるいは長さ $13$ 以下の 01-文字列をすべて走査してデータを検証する」という実験でデバッグしました。 quick link はテストできておらず、正直自信がない

その他

以上では、とりあえず実装にあたって理解したいことに絞って説明しました。説明を省いていた部分を少し回収します。

occurrence

$\mathrm{link}$ の接続関係は $\mathrm{odd}$ を根とする根付き木をなしますが、ここで回文 $v$ の部分木にわたる $\mathrm{cnt}$ の総和が、文字列中の $v$ の出現回数に等しくなります。 $\mathrm{cnt}$ の定義「接尾辞すべてについて最長の接頭辞回文を求めて並べたとき、 $v$ に対応する文字列が現れる回数」からシンプルに導けます。([1] Proposition 5.3) 「接頭辞」↔「接尾辞」で値が変わらないこと([1] Lemma 5.1)も、ここから直ちに導かれます。

direct link

ノード $v$ から $\mathrm{link}$ をたどることで、 $v$ に任意の文字 $c$ を追加したときの新しい最長回文接尾辞（を $cwc$ と表したときの $w$ ）を取得するというデータ構造を作ることができ、それを direct link ($\mathrm{dlink}(v,c)$ ) と呼びます。 $\mathrm{link}$ の木構造に注意すると、各ノード $v$ に $\mathrm{dlink}(v,c)$ をすべて保存するサイズ $\sigma$ の配列を持てばノードあたり $O(\sigma)$ 時間 $O(\sigma)$ 空間で構築できます。この場合 quick link は不要です。

ここで direct link を永続平衡二分探索木で管理すれば $\mathrm{dlink}(v,c)$ の計算量が $O\left( \min ( \log\sigma , \log \log |s| )\right)$ に改善します。しかしまあ、競プロ向きではないだろうなと思います。このような、手法による計算量の変化は [2] の 3.2.3 に表でもまとめられています。

surface の更新処理の正当性の略証明

2024-06-04 追記

([1] Lemma 2.1) 回文 $v$ について、接尾辞 $w$ が回文であるとき、またそのときに限り $v$ は周期 $|v|-|w|$ をもつ。文字単位の一致から愚直に示せます。

([1] Lemma 2.6) $\mathrm{link}(v)=w$ , $\mathrm{link}(w)=x$ , $|x|\geq 1$ とするとき、 $|v|-|w|\geq |w|-|x|$ 。 Lemma 2.1 で変形して示せます。

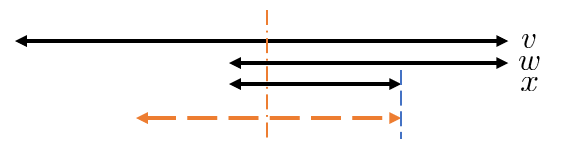
([1] Lemma 2.7 の変形) さっきの $v$ , $w$ , $x$ を下図の位置関係にとるとき、 $v$ の部分列であって $x$ と末尾位置が一致して $x$ よりも長いような回文部分列がある。

Lemma 2.6 を用いて場合分けをすれば、続く図の矢印破線のように回文部分列をとれます。

(1) $|v|-|w|\gt |w|-|x|$

(2) $|v|-|w|=|w|-|x|$

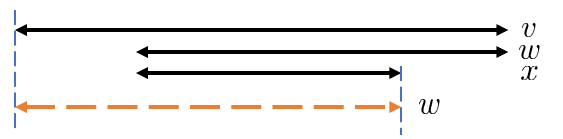
ここから本題です。

pop_back によって surface $v=\mathrm{sufsurf}(|s|)$ が失われることを考えます。新しく回文部分列は現れないので、 $v$ によって覆われていた回文部分列が新しく surface となるものを列挙すれば十分です。 $\mathrm{link}(v)=w$ とおきます。

• $s$ の末尾にある $v$ が消えることにより、その $v$ と先頭位置が一致する $w$ が新たに surface となるかもしれません。処理方法は surface の定義からほぼ直接確認できます。
• $s$ の末尾にある $w$ 、あるいはさらに link をたどった先の回文(その場合はそれを改めて $w$ とおく)が消えることにより、 $w$ と先頭位置が一致する $x=\mathrm{link}(w)$ ( $|x|\geq 1$ )が新たに surface となるかもしれません。それが起こりえないことは、直前で言及した Lemma 2.7 が示しています。

これに従って presurf, sufsurf を更新すると、 [1] Lemma 5.12 の更新式が得られます。 [1] Lemma 5.10 (pushによる surface の更新) はこれの逆操作と見ればよいです。

(*1) 論文では厳密さを欠かないようにするために、添え字を駆使した愚直な方法で書いているというように見えました。あるいは、そこだけ読めるようにするという意図があるかもしれません。たぶん手順の本質は変わらないのですが、解説向きではないね

既存ジャッジ

• queue に対して相異なる回文部分文字列を数える問題が Codeforces にあります。 上で示した実装を用いた解答

感想

証明が細かく書かれているものの、一部は自力で納得するほうが早く、直感を通すためにはそれほど手間がかかりませんでした（本投稿でもそれを信じて簡潔にしています）。（一応、使った部分は後で証明に目を通したつもりです。^(*1)）怒涛の場合分けと添え字ガチャが、ヤバい。

occurrence recording method はイントロを見てもよくわかりませんでした。

(*1)

• Lemma 5.10 の証明の sufsurf の場合分け 2.(a),(b) は添え字の $i$ , $j$ が逆になっていると思います。 $i$ が末尾か $j$ が先頭となる回文の存在を示すはず。
• Lemma 5.12 の証明の sufsurf 側の最初のほうに自明な式が書いてありますが、これはおそらく $\mathit{sufsurf}\;(s^{\prime},i)=\mathit{sufsurf}\;(s,i)$ のこと。
• Lemma 5.12 の証明の sufsurf 側の場合分け 2. の結論は $\mathit{sufsurf}\;(s^{\prime},i)=\epsilon$ ではなく $\mathit{sufsurf}\;(s^{\prime},i)=\mathit{sufsurf}\;(s,i)$ を得るべきで、これは $s^{\prime}[|s|-|t|+|t^{\prime}|-|\mathit{sufsurf}\;(s,|s|-|t|+|t^{\prime}|)|+1..|s|-|t|+|t^{\prime}|]$ が（ $s$ 中でも surface であったように） $s^{\prime}$ の surface であることから導かれると考えています。

おわり