背景
競プロでは、ユークリッド距離最小全域木の計算方法として、 Fortune のアルゴリズムでドロネー図(Delaunay diagram)を構築し、ドロネー図の最小全域木を計算するという方法がよくとられています。一方で、 Library Checker の想定解では浮動小数点数演算が現状使用不可であり、多くの Fortune のアルゴリズムの実装を流用できません。また、 Fortune のアルゴリズムで必要になる比較演算には両辺が無理数(有理数$\times$sqrt(有理数)という感じの)である場合があり、整数範囲での実装は難しいです。
ドロネー図の構築に本質的に必要な比較は「点 $D$ は、 $3$ 点 $A,B,C$ を通る円の内側にあるか?」(ここでは内外判定と呼ぶことにします)というものであり、 Wikipedia を参考にすると、次の形の比較で処理できます。( $X_k$ , $Y_k$ $k=1,2,3$ は $2$ 座標の差です。)
$$\begin{vmatrix}X_1 & Y_1 & {X_1}^2+{Y_1}^2 \cr X_2 & Y_2 & {X_2}^2+{Y_2}^2 \cr X_3 & Y_3 & {X_3}^2+{Y_3}^2\end{vmatrix} \overset{?}\gt 0$$
ただし、点の順番が反時計回りか時計回りかで不等号の向きが変わります。
入力座標が整数であれば、その $4$ 乗オーダーの大きさになるとはいえ整数範囲の演算で十分です。( Fortune のアルゴリズムのように中心座標を用いる場合、 $6$ 乗オーダーとかになると思います。) Wikipedia の同ページには複数のアルゴリズムが紹介されていますが、そのうち分割統治による方法を採用し、 correct.cpp を実装しました。
解説の前に
詳細に調べたい場合は論文を読むべきかもしれません。 Wikipedia からもリンクされている↓が該当すると思います。私は(記録していなかったので)どれくらい参考にしたか分かりません。
[1] :これの Lemma 8.1 に円の内外判定の式も書いてあります。その後ろの「9. THE DIVIDE-AND-CONQUER ALGORITHM」がアルゴリズムの説明のはずです。
アルゴリズムの前に:データ構造
平面上のグラフを表現するデータ構造が必要です。なぜなら、ある頂点に接続する辺の平面上の位置関係(角度の関係)も管理される必要があるからです。
無向辺 $1$ つに対して、双方向のそれぞれに対応する $2$ つのインスタンスを作り、ポインタ to , rev , ccw , cw を管理します。
- その辺は $u$ から $v$ への方向に対応するものとします。
toは $v$ です。revは、逆方向の辺です。ccwは、 $u$ からその辺の方向に見てから、左手方向に回って初めて見える辺です。cwは、 $u$ からその辺の方向に見てから、右手方向に回って初めて見える辺です。
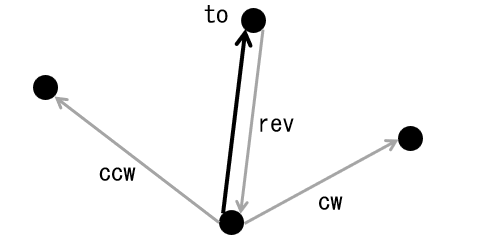
最終的に三角形分割になるので、外周以外では例えば e->ccw->rev->ccw->rev->ccw->rev = e が成り立ちます。(三角形の内側を時計回りに一周する、というイメージです)
こうすると、例えばドロネー図の外周に現れる凸多角形の周を走査できます。
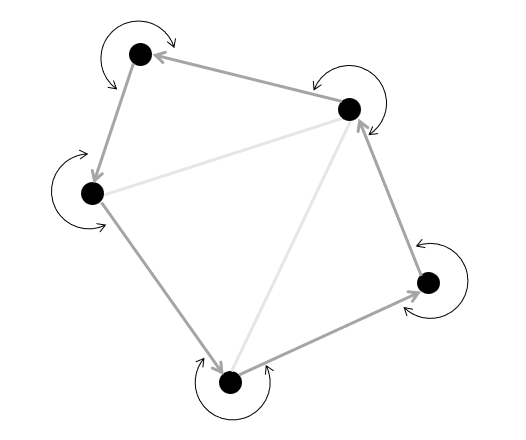
柔軟な移動のために、現在位置を表す組 $(u,e_{uv})$ を変化させることで移動を表現します。 $e_{uv}$ は頂点 $u$ から出る辺です。( $e_{uv}$ から $u$ は求まるので、 $u$ の値を持っておくことが本質的に必要というわけではありません。)
例えば、ドロネー図の外周のうち任意の $1$ 辺をスタートして、最も $x$ 座標が大きい点を見つけるという操作(getMaximum)ができます。例えば、外周を $1$ 周して頂点を列挙してしまえばよいです。
アルゴリズム
なぜ分割統治なのか?
点群を、ある直線で分断できる $2$ グループ $L$, $R$ に分けてそれぞれドロネー図を作る。このとき全体のドロネー図の構築のために追加するべき辺は、 $L$ と $R$ に $1$ つずつ端点をもつものだけである。 ([1] Lemma 7.4)(*1)
よって、左右のグループに分けてそれぞれドロネー図を作った後、それらの間の辺を構築します。 $L$ , $R$ の間の辺は、凸包の下から上へと順番に構築することができる形であることを利用して $O(n)$ 時間を達成します。これにより、全体で $O(n\log n)$ 時間になります。
下図は、 $L$ , $R$ 間の辺の様子のイメージ図です。
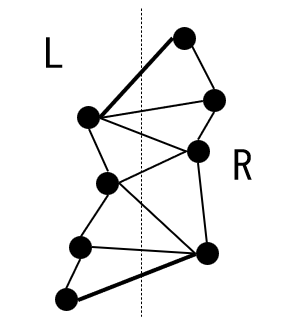
(*1) 追記:「ある直線で分断できる」という条件は [1] Lemma 7.4 では付いていないかも
メイン
次に追加する辺がどちらの方向であるか、主に内外判定を用いて判定します。
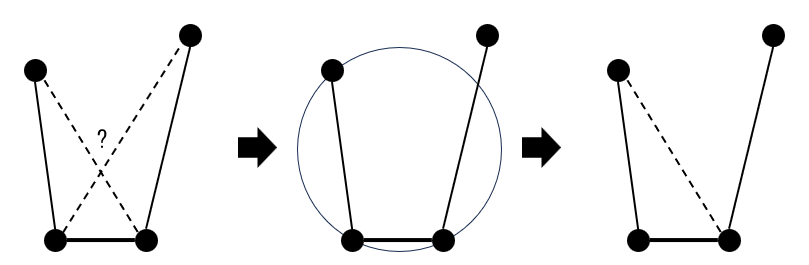
次に追加する辺がすでにある辺を食い破るかどうか、これも内外判定を用いて判定します。食い破らない場合、辺を追加します。
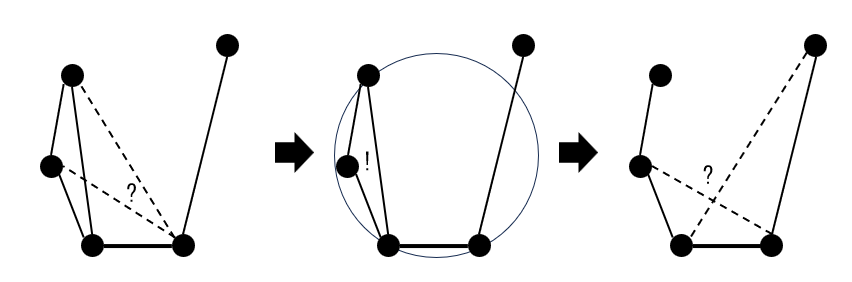
以上を繰り返して凸包の下端から上端まで辺を追加できれば、マージ完了です。
詳細
頂点数が $2$ または $3$ のときは愚直な場合分けでドロネー図を作成し、これを末尾処理として分割統治します。
凸包の上端と下端を見つけるためには、まず左グループの右端・右グループの左端を取得(getMaximum)し、そこを始点に CCW 判定を用いながらポインタを進めればよいです(goBottom)。下図はそのイメージ図で、円が各グループの凸包を表します。
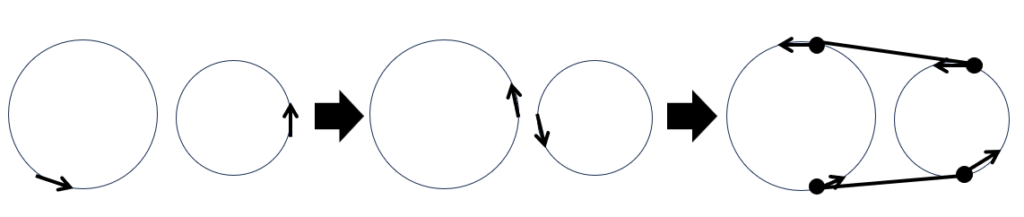
例外ケース
食い破るとグループの外に出てしまうケースがあります。この場合は食い破りの判定をスキップします。
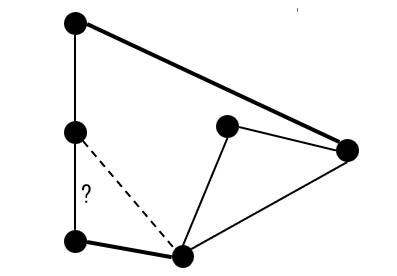
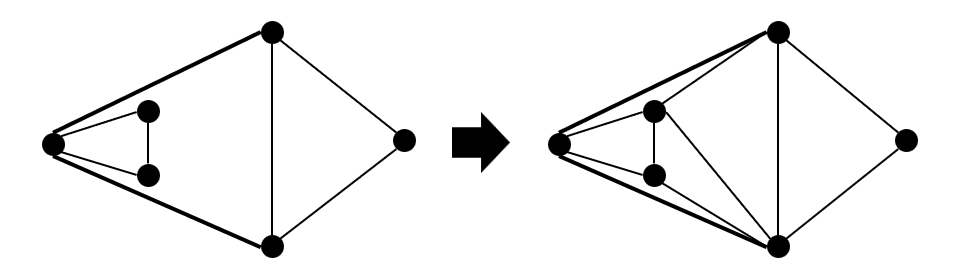
追加する辺の選び方が内外判定ではない場合があります。つまり、注目する四角形が凸であれば内外判定ですが、そうでなければ下図のように決定します。
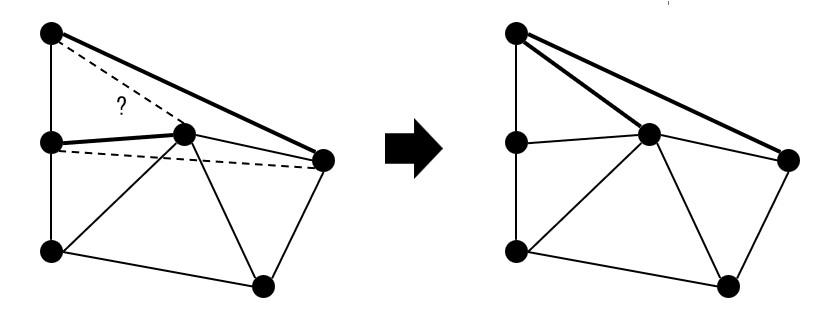
上図のケースでは、直後の食い破りの判定が変な形になりますが、内外判定の性質を確認すると、そのままでも正しい判定はできます。
凸包の上の端と下の端が頂点を共有する場合も注意すべきです。具体的な手順によってはバグります。
特にこれらに注意した実装をすると、ランダムな点群(頂点数およそ $50$ )で生成した多数のケースにおいて正しいドロネー図を構築しているかの検証を通過しました。
MST パート
元の問題では同じ座標が複数回現れる場合があるため、ドロネー図を構築する前に取り除かなければなりません。
テストケース作成について
Pull Request #1207 マージ時のテストケースは、すべて naive_prim.cpp の最終的な出力が AC を得ることを確認しています。
(終わり)