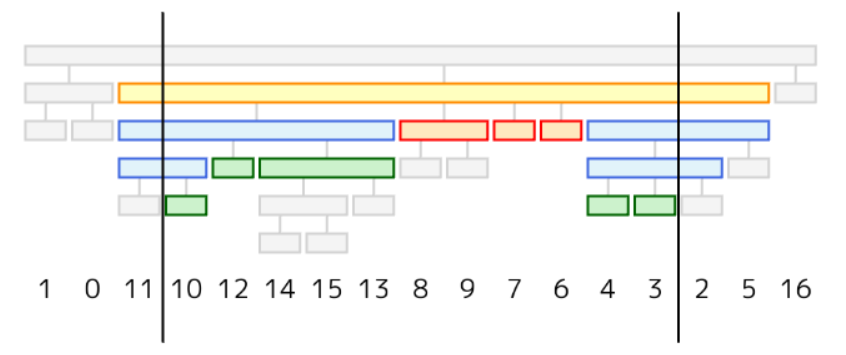
こどふぉブログ勉強月間では、 codeforces blog の積読を消化して、ついでに日本語の資料を作っておくことを目標にします。
参考資料
- Tutorial on Permutation Tree (析合树）codeforces blog, by errorgorn 、およびそれに対する複数のコメント
問題
順列が与えられたときに、 permutation tree を構築してください。定義はすぐ後で説明します。
Library Checker には “Common Interval Decomposition Tree” という名前で問題が用意されています。何でもありますね
定義と基本的性質
$(0,1,\ldots ,N-1)$ の順列 $P=(P_0,P_1,\ldots ,P_{N-1})$ に対して、以下で用語を定義します。
- $0\leq l\lt r \lt N$ について、ある $x$ , $y$ ($0\leq x\lt y\lt N$ , $y-x=r-l$ )が存在して $\lbrace P_l,P_{l+1},\ldots ,P_{r-1}\rbrace = \lbrace x,x+1,\ldots ,y-1\rbrace$ を満たすとき、 $[l,r)$ は良い区間(*1)であるとします。(*1)
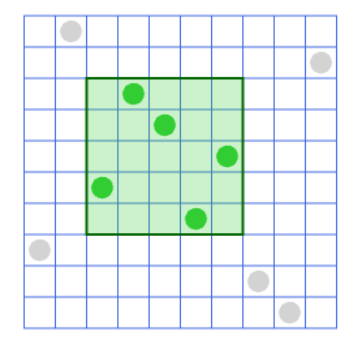
- 良い区間 $Z$ が強い良い区間であるとは、他の任意の良い区間と包含関係にあるか共通部分をもたないこととします。
- 強い区間の包含関係を表す木が permutation tree です。
- permutation Tree のノードは、次の $2$ 種類に分類されます。
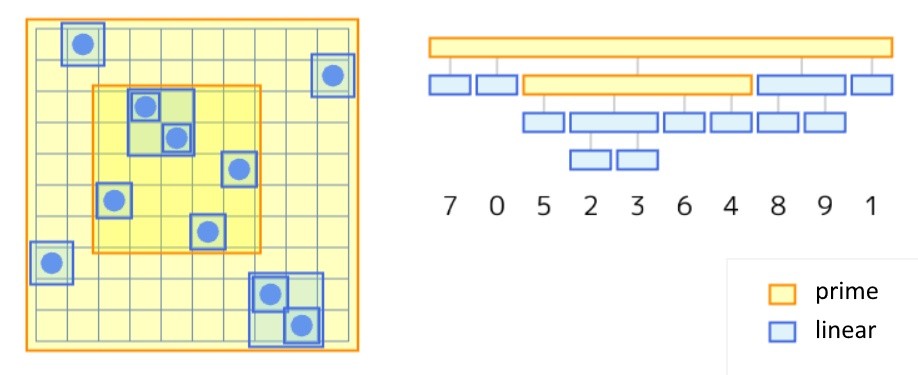
- 子の連続部分列はすべて良い区間をなす。このときのノードを linear node といいます。
- linear node でない場合、そのノードを prime node といいます。
- これに従って、強い良い区間も prime と linear に分類します。
(*1) Library Checker の問題文にあるように、 common interval と呼ぶのがいい感じというのもあると思いますが、長いので、言い換えます。
性質
- 順列全体 $[0,N)$ も、要素 $1$ 個からなる区間 $[k,k+1)$ も良い区間であり、強い良い区間です。
- prime node の子の列について、長さ $2$ 以上であって列全体でもない連続部分列は良い区間をなしません。
- $\Theta (N)$ 頂点です。
嬉しいこと
- 木構造をなす（つまり、層状である）ことが分かっているので、考察がスムーズになる場合があります。
- 難しいクエリを木クエリに帰着して処理できる場合があります。
シンプルな構築アルゴリズム
区間 $[l,r)$ が良い区間である条件は、 $$\max \lbrace P_l,P_{l+1},\ldots ,P_{r-1}\rbrace -\min \lbrace P_l,P_{l+1},\ldots ,P_{r-1}\rbrace =r-l$$ つまり $$0=\max \lbrace P_l,P_{l+1},\ldots ,P_{r-1}\rbrace -\min \lbrace P_l,P_{l+1},\ldots ,P_{r-1}\rbrace-r+l$$ と表せます。 $r$ を $1$ から $n$ まで動かすと、 $\max$ および $\min$ の変化分はそれぞれ $l$ に関する区間加算クエリで処理できます。よって、良い区間の列挙は区間最小値クエリで実現できます。
この方法を応用すると ABC248Ex – Beautiful Subsequences の想定解になります。この問題は permutation tree が元ネタになっているようです。(参考)
アルゴリズム
強い区間の列挙
少し列挙対象を広げて、良い区間 $[l,r)$ であって、ある $r\leq r^{\prime}$ に対して $[l,r^{\prime})$ が強い良い区間であるもの（これを左に強い良い区間と呼ぶことにします）を列挙します。
$r$ を $1,2,\ldots ,N$ と動かして順に処理します。
まず $[r-1,r)$ は強い良い区間です。まず $y=r-1$ として、以降は $[y,r)$ が左に強い良い区間であるという条件を保ちます。
ここで $l$ の候補が昇順に詰められた stack （つまり、降順に出てくる）があるとします。 $x$ を stack のトップ、 $y=r-1$ として始めて、以下のように処理します。
- そもそも stack が空で $x$ が取れなければ終了です。
- (1) $[x,r)$ が良い区間でなく、 $[x,r)$ に現れる値の範囲内の値が $x^{\prime} \lt x$ なる $P_{x^{\prime}}$ に現れる場合、これ以降 $x$ は強い区間の左端になりません。よって $x$ は stack から取り除き、 stack の次のトップを $x$ とおいて続けます。
- (2) それ以外で、 $[x,r)$ が良い区間でない場合、それよりも左側に長い区間（ $x^{\prime}\lt x$ として $[x^{\prime},r)$ ）も良い区間ではありません。この場合は stack の状態を保留し、今の $r$ の値に関する処理を終了します。
- (3) $[x,r)$ が良い区間である場合、 $y\gets x$ として $x$ を stack から取り除き、次の $x$ の確認に進みます。
最後に $y$ を stack に入れます。
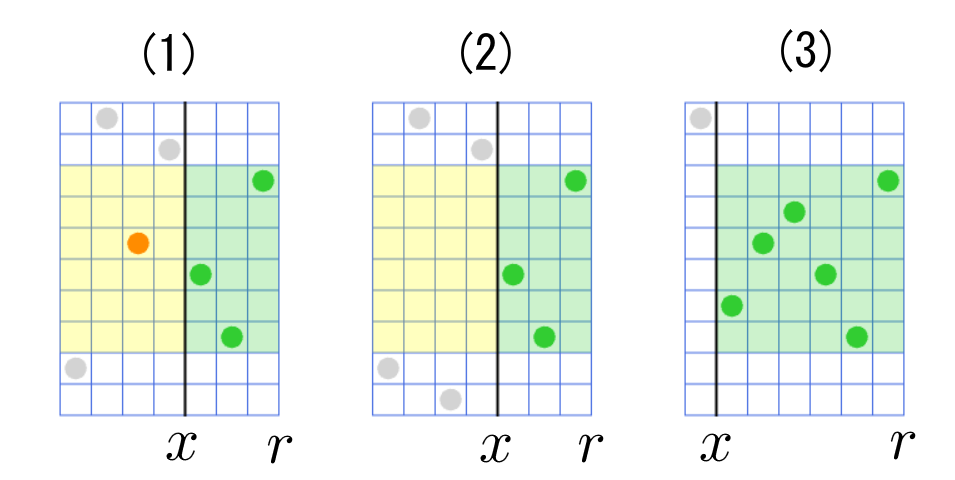
このように、強い良い区間の左端の候補は stack の操作で列挙できます。
場合分けの判定は、「 stack のトップにある区間について、値の範囲を取得」と「 $x\leq v\lt r$ に対して ${P^{-1}}_v$ の最小値は $x$ 未満であるかの判定」に帰着します。前者は値の範囲も stack に保存すれば得られます。後者は range minimum query として処理できます。 range minimum query は理論的には計算量 $\langle O(N),O(1)\rangle$ (*1) です。（競技用の実装ではこの計算量にこだわらないことをお勧めします。）
(*1) 前処理の時間計算量が $O(N)$ 、オンラインクエリで最悪時間計算量 $O(1)$ です。
permutation tree の構築
左に強い良い区間を短い順に確認します。ここで、 $n$ 要素の単方向連結リストを用意しておき、良い区間が見つかったら対応する区間内の要素を削除し、単方向連結リストに残っている要素が現時点で確認済みの極大な左に強い良い区間を表すようにします。
ここで、
- prime な強い区間は、 $2$ つの左に強い良い区間に分割されない。
- それ以外の左に強い良い区間であって長さが $2$ 以上のものは、 $2$ つの左に強い良い区間に分割できる。
という性質から、強い良い区間の種類を簡単に判断できます。
問題解答例
これまでにどこかしらの競技で出題された問題の例。
問題： Codeforces Round #493 Div.1 E. Good Subsegments
順列がまず与えられます。クエリでは $l,r$ が与えられるので、順列中の良い区間のうち $[l,r)$ に収まるものの個数を求める、という問題です。
考慮する必要がある強い区間について集計します。詳細の説明は省きますが、下の図で色分けされているように分類して集計すればよいです。
後は木クエリとして処理できます。計算量は $O((n+q)\log n)$ (理論的には $\langle O(n),O(1)\rangle$ (*2) ) になります。
(*1) 図に示されている例では、すべてのノードは linear node です。
(*2) lowest common ancestor および level ancestor の計算量が $\langle O(n),O(1)\rangle$ であることを利用します。
他の問題の例：