Library Checker 解説 永続queue (Persistent Queue)

体系的な解説はほとんどできていないと思います。それでもよければ

永続 queue とは

これのことです↓

Library Checker
Library Checker
judge.yosupo.jp

永続 stack

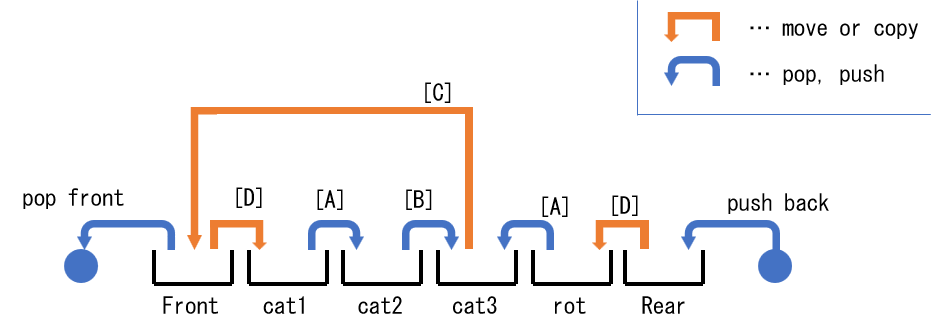
前提知識です。 pop back した後の stack へのポインタを管理すれば ok です。後で使うので、要素数も管理します。

C++ コード
struct Stack {
    std::shared_ptr<Stack> nx;
    int sz = 0;
    Elem top;

    using Inst = std::shared_ptr<Stack>;

    Stack(Inst _nx, Elem elem)
        : nx(_nx)
        , sz(Stack::size(_nx) + 1)
        , top(elem)
    {}
    ~Stack() = default;

    // cur に pop back した後の状態を取得
    static Inst pop(const Inst& cur){
        return cur->nx;
    }

    // cur に push back した後の状態を取得
    static Inst push(const Inst& cur, const Elem& x){
        return std::make_shared<Stack>(cur, x);
    }

    // 要素数
    static int size(const Inst& cur){
        return cur.get() ? cur->sz : 0;
    }
};

queue に push front を追加する拡張

front 側に永続 stack をつなげれば push front に対応できるようになります。

C++ コード
struct ExPersistentQueue {
    PersistentStack f;
    PersistentQueue q;

    Elem top() const { return Stack::size(f) ? f.top() : q.top(); }

    ExPersistentQueue pop_front() const {
        ExPersistentQueue res = *this;
        if(Stack::size(res.f)){
            res.f = res.f.pop();
        } else {
            res.q = res.q.pop();
        }
        return res;
    }

    ExPersistentQueue push_front(Elem e) const {
        ExPersistentQueue res = *this;
        res.f = res.f.push(e);
        return res;
    }

    ExPersistentQueue push_back(Elem e) const {
        ExPersistentQueue res = *this;
        res.q = res.q.push(e);
        return res;
    }

    int size() const { return res.f.size() + res.q.size(); }
};

O(log N) 時間, O(log N) 空間

時間・空間計算量ともに $O(\log N)$ ($N$ は queue の要素数)を許せば、 binary lifting で実装できます。

queue のインスタンスは以下の情報を持ちます。

  • 最後の要素の値
  • queue のサイズ $z$
  • $2^d\leq z-1$ を満たす非負整数 $d$ について、 $2^d$ 個手前の要素 $A_d$ へのポインタ

そうすれば、 push back のときの新しい $A_d$ は $d$ の昇順に求まります。 top は binary lifting によって処理できます。 pop front は $z$ を更新した新しいインスタンスを作ればよいです。

この方法による、過去の私(Nachia)の解答があります： #39108

償却定数時間

queue を front (front 側)、 rear (back 側) の $2$ つに分け、それぞれ stack $F$ , $R$ で管理します。それぞれ stack の出入口が queue の端側になります。 queue 全体は $F+{}\!\!\!\! {}+\mathrm{rev}(R)$ で表せます。( $+$ はリストの連結で、 $\mathrm{rev}$ は reverse です。)

操作途中で、サイズについて $|F|+1=|R|$ となったとき、 $F\leftarrow F+{}\!\!\!\! {}+ \mathrm{rev}(R)$ という操作の遅延評価を予約します。

遅延評価を予約するとき、組 $(F,R)$ を持つ構造体を作ります。これを保持しつつ、 $F+{}\!\!\!\! {}+ \mathrm{rev}(R)$ の出入り口側から構築し、 $F$ が尽きたら $\mathrm{rev}(R)$ を評価して連結します。(*1)

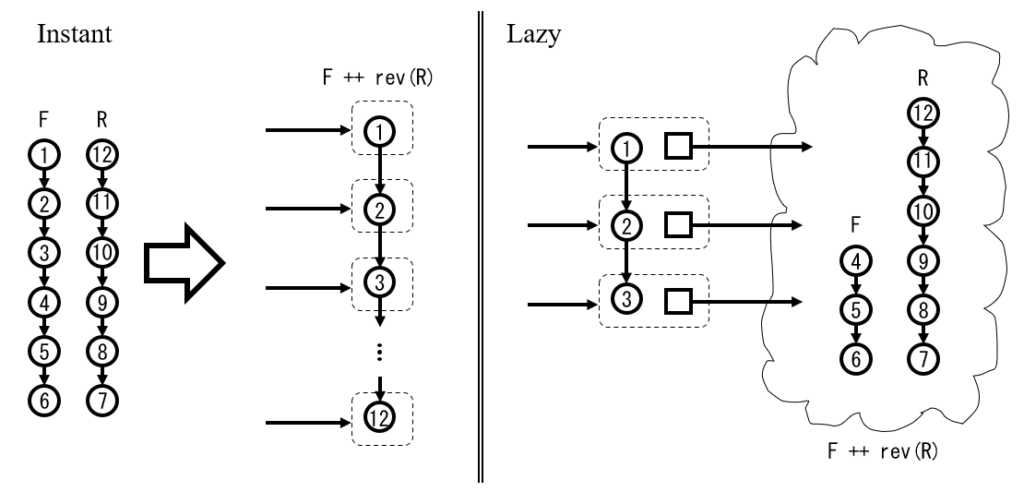
上の図において、左側は $F+{}\!\!\!\! {}+ \mathrm{rev}(R)$ を完全に評価して得られる stack 、右側はそれを途中まで評価した状態を表します（実線矢印はポインタ）。「最終的に左図を得たい、途中まで作ったのが右図」ということです。必要になり次第、 $3$ の次に $4$ 、 $4$ の次に $5$ というように繋げてゆき、 $6$ の次が必要になったときに $\mathrm{rev}(R)$ を評価して $7$ から $12$ までを繋げます。

本当は遅延評価の構造が再帰してもよい(Banker’s Queue)のですが、以降の説明に不要なので取り上げません。

参考実装：デWiki からリンクされている noshi さんのリポジトリ

(*1) このように、「次のノード」を次々に取得するデータ構造（図中では綿の形で示したもの）は stream と呼ばれます。たぶん。

最悪定数時間

Real-time Queue

遅延評価の処理を適切に分割し、 queue の操作ごとに少しずつ実行すれば計算量の償却が不要になります。 queue の操作を行うたびに $\mathrm{rev}(R)$ のための stack の要素の移し替えを $1$ 回分と $F$ 側の構築を $1$ 回分だけ処理すれば十分、すなわち次の遅延評価を呼び出す時には前の $F+{}\!\!\!\! {}+ \mathrm{rev}(R)$ の評価が完了しています。

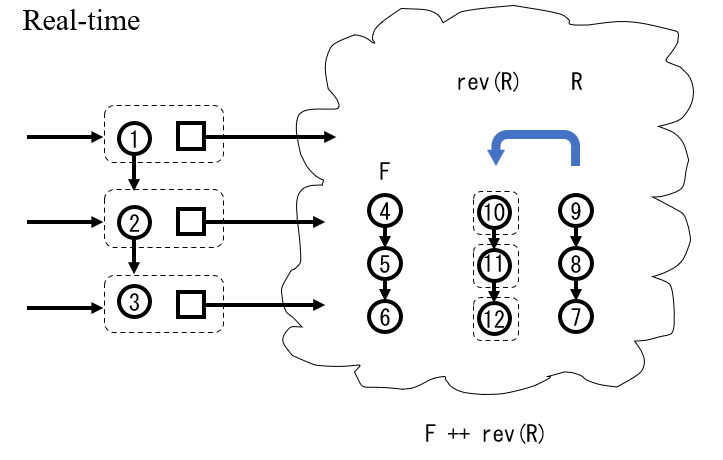
stack から実装する

「遅延評価」が実際に何をやっているのかが理解できず、唸りながら考えて実装したものです。

説明（クリックで展開）

ここまでの実装方法では、 stack を出入り口側から順に構築する、一般の stack の操作ではない操作を利用します。一方で、 front を $2$ 回反転しつつうまくやれば、永続 stack の操作のみで永続 queue を実装できます。例えば構造と不変条件を以下のようにします。

  • queue のインスタンスは、 6 個の stack (Front, cat1, cat2, cat3, rot, Rear) と、Front 連結後のサイズを表す整数値 1 つで構成されます。
  • 要素数 $0$ の場合、すべての stack は空とします。
  • 要素数 $1$ 以上の場合、 Front 連結後のサイズは Rear のサイズよりも大きいという条件を保ちます。（ front 連結後のサイズを値で持っておくとします。）
  • [A] : push back か pop front が起こるたびに、 rot から cat3 へ、また cat1 から cat2 へ要素の移動を $1$ 回ずつ行います。要素数が同じなので、移し替えは同時に終わります。
  • [B] : [A] の処理が終わった後、連結が完了していない（ cat3 のサイズが連結後のサイズより小さい）場合、 cat2 から $1$ 個供給します。
  • [C] : Front 連結後のサイズと cat3 のサイズが等しくなったら、直ちに cat3 を Front に移動します。
  • [D] : Front 連結後のサイズと Rear のサイズが一致したら、直ちに次の連結に備えます。

こうすると、

  • Front を使い切る場合、 rot→cat3 の操作によって新しい Front が完成します。
  • Front を使い切らない場合、 push back ごとに行われる操作に注目すると、 cat3 のサイズを Rear のサイズ以上に保てることになり、 [D] が発生するまでに新しい Front の用意が間に合います。

というわけで queue を実装できます。

実装： Library Checker 提出 #227039

それは本当に最悪定数時間？

理論的な計算量では、メモリの解放が無視されます。参照カウンタで実装する場合、解放順によっては $1$ 回の解放呼び出しから連鎖して多数の要素のメモリが解放される場合があります。

“Purely Functional Data Structures” の紹介

Chris Okasaki. “Purely Functional Data Structures” という資料があります。 PDF が公開されています。 : https://www.cs.cmu.edu/~rwh/students/okasaki.pdf

同じ名前の書籍もあって、これは翻訳版があります。 (Amazon)

永続データ構造の設計法が体系的にたくさん解説されているので、これで勉強しつつ投稿を書ければよかったのですが、 PDF で読みかけたところプログラム例等が関数型プログラミングの視点で(*1)書かれているなどで難しすぎたので、ここでは資料を紹介するだけにします。(*2)

(*1) この参考書はそういう目的だ、という私の認識が正しければ。
(*2) すみません…

その他の参考文献

タイトルとURLをコピーしました