トーナメント 32→16 で敗退しました。残念。
ビジュアライザのデザインの紹介
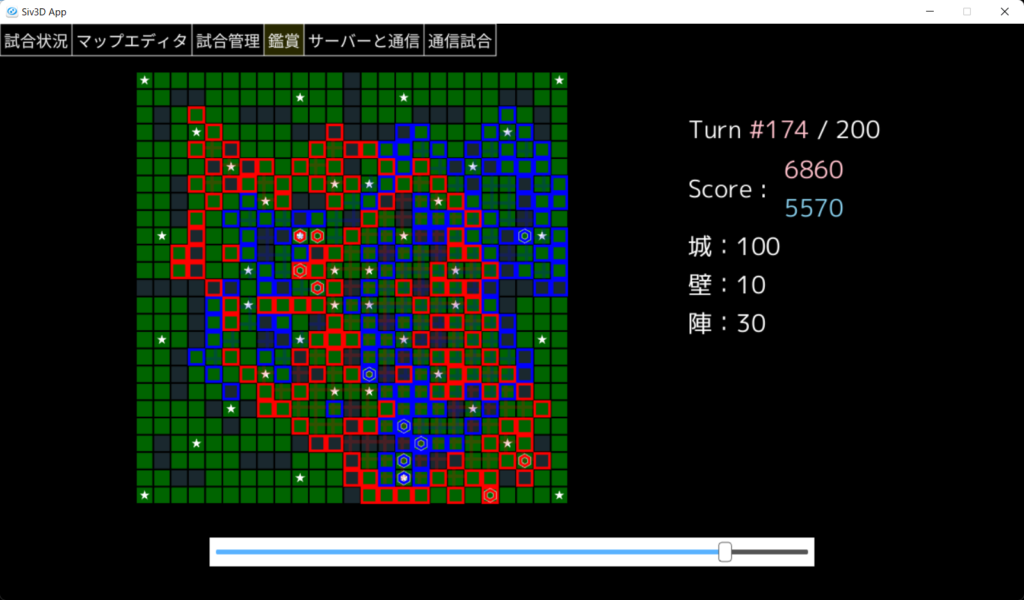
- 比較的明るくないマスが池を表します。
- 白い星印が城を表します。
- 城壁は、マス内側に四角の枠を描画して表現します。
- $6$ 角形は職人を表します。
- 陣地は、半透明でクロスを描画することで表現します。赤と青で位置をずらしています。
- 下部のスライドバーを操作することで過去のターンを参照します。
メインアルゴリズム
見込まれる陣地獲得によって得られる得点および実現可能性を利得で表現して、その利得を最大化することで効率的な陣地獲得を狙います。このとき厳密性をいくらか失う変形を入れることで計算を簡単にします。このアルゴリズムでは特に、あと数手で大きい陣地が獲得できるような状況を見逃しにくくなると考えられます。
理論
まず、各領域(=マス) $(x,y)$ について、その領域を陣地にできる場合の利得 $w_{x,y}$ $(\gt 0)$ を設定します。また、累積和 $W_{\text{e},x,y}=w_{0,y}+w_{1,y}+\cdots +w_{x-1,y}$ を計算しておきます。
累積和を参照しながら見込み陣地の外周を反時計回りにたどると、陣地全体の利得が計算されます。このとき移動の分岐点である(領域の四隅にあたる)場所を「ターミナル」と呼ぶことにします。
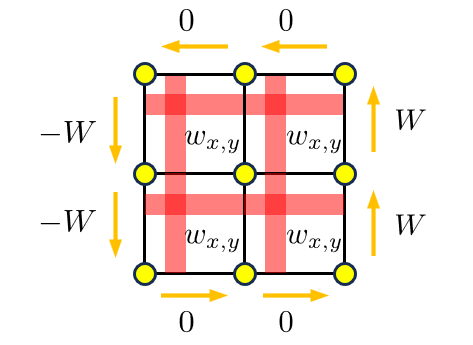
これをもとに、城壁を建設したときのターミナルの移動および利得の寄与を考えます。「城壁の内側を反時計回り」でカウントするためには、城壁中心で考えれば利得は常に時計回りで加算しなければなりません。(下図) $1$ つの城壁を建設するときのターミナルの移動は ${}_4\mathrm{P}_2=12$ 通り考えられます。
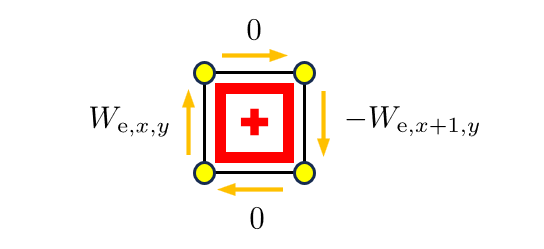
新しく建設する城壁が他の城壁と連結になる場合を考えます。ほかの城壁が連結な部分は、あらかじめターミナルを併合しておきます。ここで、すでに城壁が存在したり、すでに閉じた陣地になっている領域の利得を $0$ に設定すれば、城壁で連結している部分のターミナルの移動は城壁のどの側を通っても利得の変化が一定になり、これらのターミナルを併合してしまっても利得の計算が整合します。
すでに城壁がある部分について代表のターミナルを選び、各ターミナル $(x,y)$ について、 $(x,y)$ からその代表のターミナルへ移動するコスト $J_{x,y}$ を事前に計算します。すると城壁を建設するときの利得の寄与は、併合されたターミナル内の移動 $2$ 回と建設する城壁のまわりの移動 $1$ 回で表せるため、 $O(1)$ ステップで計算できます(下図)。
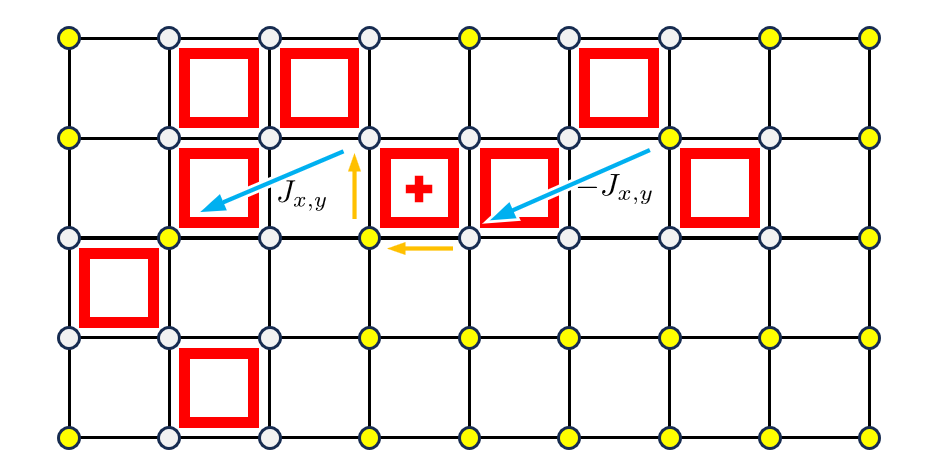
計画中において、 $1$ 体の職人は城郭の反時計回りの順に城壁を建設すると仮定します。(時計回りの場合も同様にできます。)すると城郭形成による利得への寄与が、ターミナル間の移動による利得の総和で表せて、建設する順番に計算できます。まさに、ターミナルを頂点とするグラフの重み付き経路に対する問題です。
職人の移動も計画に含められるようにします。
まず、各ターミナルについてその時点の職人の位置でノードを分割し、「ターミナルの位置と職人の位置」に対してノードを設定します。ターミナルと職人が離れている以外は省略します。併合されたターミナルでは、構成するターミナルそれぞれで分けた後、同じものをまとめます。
下図は、同じターミナルを見ていながら職人が移動するような遷移のイメージです。
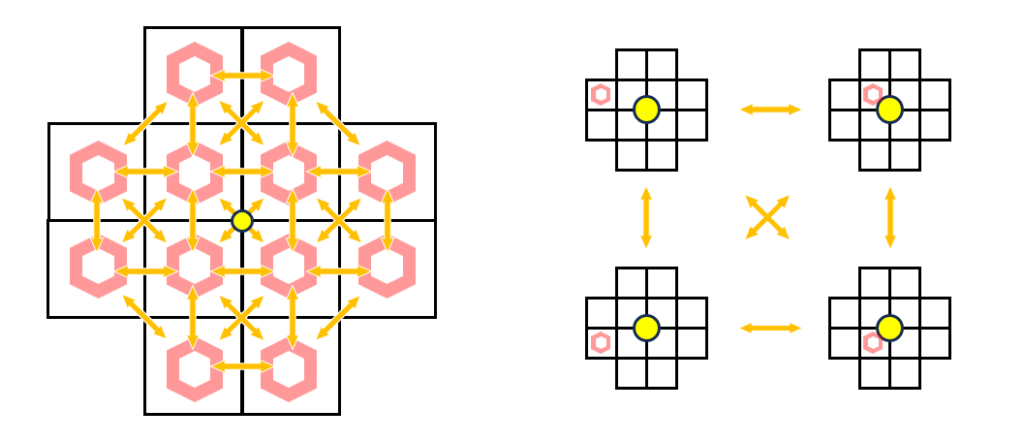
移動先や建設位置に相手城壁が存在する場合は操作列に解体を付けて $2$ ターン分として遷移します。場合によっては利得を特別に加算します。
以上、計画に利用する操作を $1$ ターン以上かかる操作に分解し、経路問題に帰着しました。これを解くことで、自陣職人の $q$ および始点ターミナル $u$ 、終点ターミナル $v$ 、必要ターン数 $t$ $(1\leq t \leq 10)$ について
- 職人 $q$ が $t$ ターンの間の動作してターミナル $u$ からターミナル $v$ まで(反時計回り・あるいは時計回りで)城郭を築く場合の利得寄与の最大値 $G_1(q,t,u,v)$ 、およびそのための最初の操作
が得られます。(ターミナル $u$ 周辺までの移動は別で計算することで、職人 $q$ の初期位置がターミナル $u$ から離れている場合も計算に含めます。)基本操作が $1$ ターン以上かかるので、(ダイクストラ法などではなく)動的計画法ですべて計算できます。ターミナルの組 $(u,v)$ は限られるので適切にテーブルを省略します。
これが得られれば、ターミナル $s$ から始めて $s$ で終わる経路 $s\rightarrow p_1\rightarrow \cdots \rightarrow p_k \rightarrow s$ を複数の職人で構築すればよいです。よって、自陣職人の部分集合にわたる動的計画法をして
- 自陣職人のうち $S$ に含まれるものが $t$ ターンの間の動作して、ターミナル $u$ からターミナル $v$ まで城郭を築く場合の利得寄与の最大値 $G_2(S,t,u,v)$
を計算し、 $u=v$ の部分を見れば、利得を最大化した計画が得られます。
成功例
下図は、ファーストステージ前半第2試合表において逆転が起きたターンから(後手番を数えて) $2$ ターン前の状態です。

アルゴリズムを適用することで、 $3$ 体の職人が動作することで $2$ ターンで陣地を獲得できるような計画を立てることができます。(下図)

利得のバリエーション
計画に対して、陣地獲得見込み以外に以下のような利得の設定が可能です。
- $t$ ターン目に職人が領域 $(x,y)$ に侵入するような移動をする場合、利得 $f_1(t,x,y)$ を加算。
- $t$ ターン後に職人が領域 $(x,y)$ に存在する場合、利得 $f_2(t,x,y)$ を加算。
- $t$ ターン目に領域 $(x,y)$ に城壁を建設する場合、利得 $f_3(t,x,y)$ を加算。
その他のアルゴリズム
単に、適当に選んだ位置に城壁を建設しに行きます。建設位置までの移動には、メインで使ったものを使いまわします。
ソースコード
GitHub:
ギリギリで実装したので危ないですが、メインはちゃんと実装できているはずです。
並列化したときに時々クラッシュするようになってしまったので何かが失敗しています。