ABC288D を見て言っています
ハッシュ使えよ、という方はこちらへ → → → ABCのユーザー解説
問題概要
数列 $A_0=(A_0[0],A_0[1],\ldots ,A_0[K-1])$ が与えられる。次の形式の操作を $i=1,\ldots ,N$ に対して行い、 $N$ 個の新しい数列 $A_1,A_2,\ldots ,A_N$ を生成する。
- $A_{i-1}$ から、 $A_{i-1}[x_i]$ を $y_i$ に書き換えて得られる数列を $A_i$ とする。
$x_i$, $y_i$ は与えられる。得られる $N+1$ 個の数列を辞書順でソートし、一致関係で分類せよ。
$K=O(N)$ として、 $O(N\log N)$ 時間。
方法
数列のソートに利用する分割統治法
要素に順序がついた列 $X$ が与えられたとき、 $X$ の大小関係を保ったまま、できるだけ小さい非負整数からなる列を得ることを、座標圧縮といいます。
列 $X^\prime$ , $Y^\prime$ をそれぞれ座標圧縮した数列 $X$ , $Y$ (合計長さ $n$ )が与えられたとき、 $X$ の要素 $x$ と $Y$ の要素 $y$ から組 $(x,y)$ をたくさん作ったものを辞書順ソートしたいとします。これは $Y$ でバケツソートしたあと、 $X$ でバケツソート(安定ソート)をすると $O(n)$ 時間で実現します。よって、座標圧縮も $O(n)$ 時間です。
だから、長さが一定の数列の列を辞書順ソートしたい場合、各数列を $2$ 分割し、前半と後半をそれぞれソートしてからそのペアをソートするという分割統治法が考えられます。
変化する点が O(N) 個なので
まず、数列上の位置ごとに、現れる値を座標圧縮しておきます。
数列の要素が変化するところが $N$ 回しかないので、上の分割統治法で分割する過程で現れる数列たちに関して、数列が変化する回数は延べ $O(N\log K)$ になります。よって、ソート対象をランレングス圧縮すると、現れる数列の合計個数が $O(N\log K)$ になります。これを利用して分割統治法を実装すると、目的のソートを $O(N\log N)$ 時間で得ます。
例
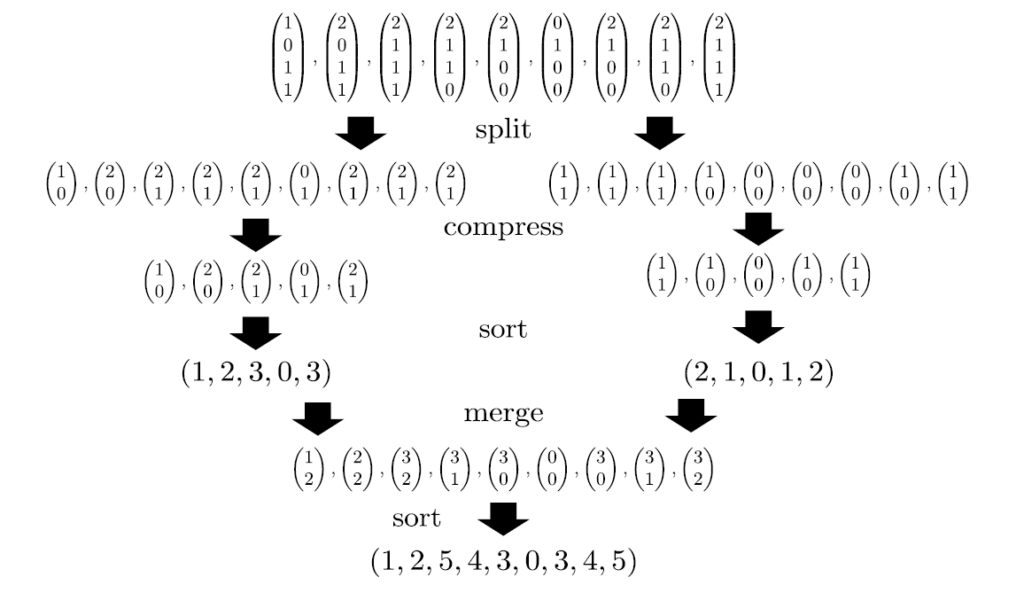
使用例
(2023/09/18) ABC238G を追記しました。
ABC288D
Toyota Programming Contest 2023 Spring Qual A(AtCoder Beginner Contest 288) D – Range Add Query

ABC238G
モノグサプログラミングコンテスト2022(AtCoder Beginner Contest 238) G – Cubic?
変更比較の対象となる配列は、与えられる数列の要素 $1$ 個あたり $O(\log A)$ 点で変化するため、 $K=\pi (A)+N\log_2 A$ としたとき配列の辞書順ソート結果は $O(K \log K)$ 時間で計算できます。ここで、配列の要素が $0,1,2$ の値しかとらないので、 $w/2$ 以下の素因数を $1$ ワード(配列の単一要素)で処理することで、 $K=\pi (A)+N+N\frac{\log_2 A}{\log_2 w}$ と変えることができます。