転置原理まとめ

競プロやってても使わないテクニック

転置原理とは

転置原理(Tellegen’s Principal)は、アルゴリズムの変形方法です。主に多項式関連の問題で利用され、応用例は現在 (2024年) も拡大しています。

競技プログラミングにおける解法の導出方法としては現状極めてマニアックなものですが、導出されたアルゴリズムをサブルーチンとして実装して利用することがあります。

• Bostan, Alin, Grégoire Lecerf, and Éric Schost. “Tellegen’s principle into practice.” Proceedings of the 2003 international symposium on Symbolic and algebraic computation. 2003. (ResearchGate)

行列の転置

ここでは行列 $A$ の転置を $A^T$ と表します。

$N\times M$ 型行列の転置は、 $(i,j)$ 成分の値を $(j,i)$ 成分に移動させて得られる $M\times N$ 型行列です。

$${\begin{pmatrix}1&2&3\cr 4&5&6\end{pmatrix}}^T=\begin{pmatrix} 1&4\cr 2&5\cr 3&6 \end{pmatrix}$$

一般の行列の転置について、

$$(AB)^T=B^TA^T$$

が成り立ちます。 $3$ 個以上の行列積の場合は、

$$(AB\cdots YZ)^T=Z^TY^T\cdots B^TA^T$$

のように、各行列を転置して掛ける順番を反転することで等しい行列を得ます。

問題の転置

さて、計算問題にはベクトルと行列の積で表せるものがあります。 $\bm{v}$ を入力、 $\bm{w}$ を出力として、 $\bm{w}=A\bm{v}$ という関係があるとします。この問題を転置した問題(以降、転置問題と呼ぶ)とは、 $\bm{x}$ を入力、 $\bm{y}$ を出力として $\bm{y}=A^T\bm{x}$ と表される問題です。転置によって入力と出力のサイズが入れ替わることに注意するとよいです。

$$\bm{w}=A\bm{v}\xleftrightarrow{\quad\text{転置}\quad}\bm{y}=A^T\bm{x}$$

ここで $A\bm{v}$ の計算過程を分解して次のように行列積で表せたとします。

$$\bm{w}=A\bm{v}=BC\cdots YZ\bm{v}$$

行列の転置の性質より、転置問題について

$$\bm{y}=A^T\bm{x}=Z^TY^T\cdots C^TB^T\bm{x}$$

が成り立ちます。

アルゴリズム設計への応用

本投稿の後半部で例示するように、分解後の基本的なベクトル-行列積の計算は、通常、その転置も同じ計算量で計算できます。これにより、

$$\bm{w}=A\bm{v}=BC\cdots YZ\bm{v}$$

の計算方法から

$$\bm{y}=A^T\bm{x}=Z^TY^T\cdots C^TB^T\bm{x}$$

の計算方法を導くことができ、さらにそれらは原理的には定数倍を含め同じ計算量^(*1) のものになります。これにより、

• 解きたい問題に対して、非自明だったアルゴリズムを、転置問題から得る
• 異なる問題（ある問題とその転置問題）の解法・計算量を統一して示す

ということができるようになります。

具体的な問題に対しては、まず入力パラメータを

• $A$ に埋め込まれるパラメータ
• 入力 $\bm{v}$

に分け、

• (ア) $A$ 内部に関する事前計算
• (イ) $A$ による変換を分解した基本的な計算

を設計します。転置問題を解くアルゴリズムを得るには、

• 先に (ア) を計算し、
• (イ) をすべて転置で置き換え、
• それを逆から実行する

とすればできます。以降では変形例を見ていきましょう。

(*1) 基本演算とその転置先が一対一対応し、原理的には演算コストは全く同じになるようですが、もちろんそれが実際の計算機・最適化された実装において全く同じ演算コストであるとは限りません。特に重要な例外としては、事前計算との兼ね合いによって、必要な空間がオーダーレベルで異なるといったことが起きます。

重み和の転置

入力がたくさん・出力が $1$ つの問題が、転置原理を適用できるアルゴリズムで解けるとします。転置原理によると、次の $2$ つは同じ計算量で計算できます。

$$\begin{pmatrix}w\end{pmatrix}=\begin{pmatrix}W_0 & W_1 & \cdots & W_{n-1} \end{pmatrix} \begin{pmatrix}v_0 \cr v_1 \cr \vdots \cr v_{n-1} \end{pmatrix}$$

$$\begin{pmatrix}y_0 \cr y_1 \cr \vdots \cr y_{n-1} \end{pmatrix}=\begin{pmatrix}W_0 \cr W_1 \cr \vdots \cr W_{n-1} \end{pmatrix} x$$

後者に対して $x=1$ を入力すると $W_0,W_1,\ldots ,W_{n-1}$ の値が具体的に得られることになり、計算結果の質が上がります。

アイデアはここから : maspy さんのツイート (https://twitter.com/maspy_stars/status/1776260037620682959)

基本的な変形

並べ替え (permute)

並べ替えの転置は、逆順列による並べ替えです。ちなみに、「転置行列と逆行列が等しい」は直交行列の定義です。

deposit ←→ extract

deposit （埋め込む操作）と extract （取り出す操作）は互いに転置です。

$$\text{deposit: }\begin{pmatrix} \bm{x} \cr \bm{0} \end{pmatrix}=\begin{pmatrix} E \cr O \end{pmatrix} \bm{x}$$

$$\text{extract: }\bm{v}_0=\begin{pmatrix} E & O \end{pmatrix} \begin{pmatrix} \bm{v}_0 \cr \bm{v}_1 \end{pmatrix}$$

add ←→ copy

コピーと加算は互いに転置です。

$$\text{copy: }\begin{pmatrix} \bm{x} \cr \bm{x} \end{pmatrix}=\begin{pmatrix} E \cr E \end{pmatrix} \bm{x}$$

$$\text{add: }\begin{pmatrix}\bm{v}_0+\bm{v}_1\end{pmatrix}=\begin{pmatrix} E & E \end{pmatrix} \begin{pmatrix} \bm{v}_0 \cr \bm{v}_1 \end{pmatrix}$$

定数倍

要素ごとの定数倍は対角行列で表されるため、自身が転置です。

$$\text{mult}\; \bm{a}\text{: }\quad \bm{w}=\text{diag}(a_0,a_1,\cdots ,a_{n-1})\; \bm{v}$$

DFT ←→ DFT

離散フーリエ変換 (DFT) は対称行列で表されるため、自身が転置です。逆変換も同様です。

$$\text{DFT}_n=\begin{pmatrix}\omega^{ij}\end{pmatrix} = \begin{pmatrix}\omega_n^{0} & \omega_n^{0} & \omega_n^{0} & \cdots & \omega_n^{0} \cr\omega_n^{0} & \omega_n^{1} & \omega_n^{2} & \cdots & \omega_n^{n-1}\cr\omega_n^{0} & \omega_n^{2} & \omega_n^{4} & \cdots & \omega_n^{2(n-1)} \cr \vdots & \vdots & \vdots & \ddots & \vdots \cr \omega_n^{0} & \omega_n^{n-1} & \omega_n^{2(n-1)} & \cdots & \omega_n^{(n-1)(n-1)}\end{pmatrix}$$

( $\text{DFT}_n$ は長さ $n$ の DFT に対応する行列、 $\omega_n$ は適切な定数^(*1) )

(*1) 数論変換のときにここの条件が重要になります。数論変換の解説を参考にしてください。 $1$ つ挙げます。 Mathlog「離散フーリエ変換と数論変換 (5) 数論変換 (NTT)」(さかぽん より)

FFT 周辺（周波数領域で添え字にビットリバーサルがかかる場合）

Cooley–Tucky のアルゴリズムでは周波数領域でビットリバーサルがかかるため^(*1)注意が必要です。

ここで、 IDFT ( Inverse DFT , DFT の逆変換) が「 $\times\frac{1}{n}$ → 先頭以外を reverse → DFT 」と等価であることに注目すると、 FFT の転置は「 IFFT → 先頭以外を reverse → $\times n$ 」と表せます。 IFFT を利用することにより、周波数領域での並び順の設定で破綻しなくなります。

(*1) 実装例として、 Tiramister’s Blog 「Cooley-Tukey Algorithm」 のプログラム例における ufft が該当します。 AtCoder Library の内部実装も該当します。

サブルーチンの転置の例

畳込み ←→ middle product

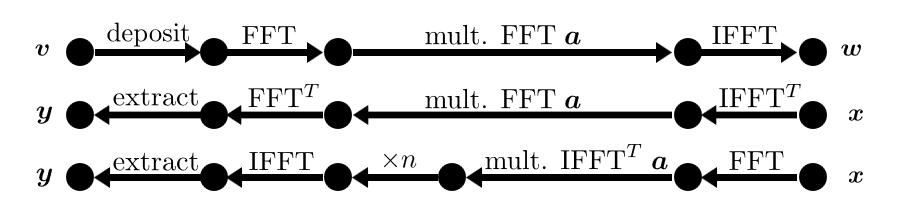
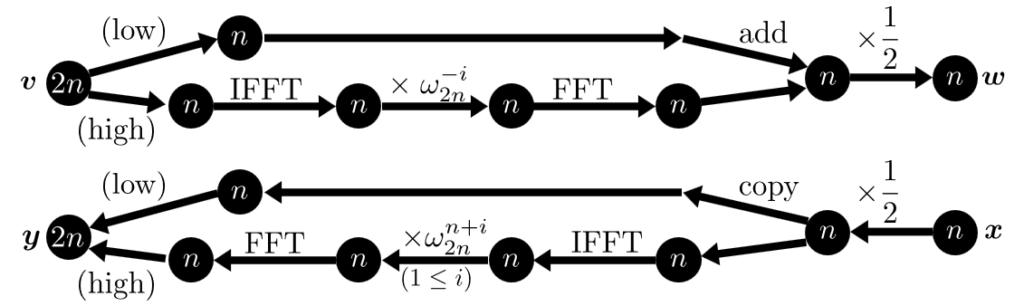
FFT doubling ・ 周波数領域から下位桁取り出し

（※ $\text{FFT}$ , $\text{IFFT}$ は周波数領域でビットリバーサルがかかっているものとします。）

(A) FFT doubling

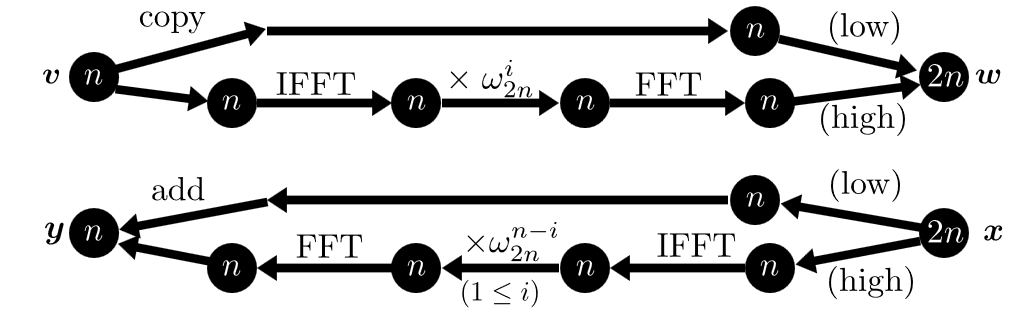
(B) 下位桁取り出し

subset convolution

n = int(input())
v = list(map(int,input().split()))
a = list(map(int,input().split()))
w = [0] * (2**n)
for i in range(2**n) :
    for j in range(2**n) :
         w[j] += v[i] * (a[j & ~i] if (i & j) == i else 0)

y[i] += x[j] * (a[j & ~i] if (i & j) == i else 0)

# (1)
y[i] += x[j] * (a[~i & j] if (~i & ~j) == ~j else 0)

# (2)
y[~i] += x[~j] * (a[i & ~j] if (j & i) == j else 0)

応用例

多点評価 ←→ 重み付き累乗和

$n-1$ 次多項式 $f(x)$ を $m$ 個の点 $x=x_0,x_1,\ldots ,x_{m-1}$ で評価した値 $y_k=f(x_k)$ ($k=0,1,\ldots ,m-1$) を計算します。 $f$ の係数を入力とすると、計算はベクトル-行列積で表せます。

$$\bm{y}=\begin{pmatrix} y_0 \cr y_1 \cr \vdots \cr y_{m-1} \end{pmatrix}=\begin{pmatrix}{x_0}^0 & {x_0}^1 & \cdots & {x_0}^{n-1} \cr {x_1}^0 & {x_1}^1 & \cdots & {x_1}^{n-1} \cr\vdots & \vdots & \ddots & \vdots \cr {x_{m-1}}^0 & {x_{m-1}}^1 & \cdots & {x_{m-1}}^{n-1} \cr\end{pmatrix}\begin{pmatrix} [x^0]f \cr [x^1]f \cr \vdots \cr [x^{n-1}]f \end{pmatrix}$$

特に $m=n$ のとき、この行列はヴァンデルモンド行列 $V$ です。

転置問題は $\bm{v}$ を入力として $\displaystyle w_i = \sum _{k=0}^{m-1} {x_k}^i v_k$ を計算する問題です。これは FPS $\displaystyle\sum_{k=0}^{m-1} \frac{v_k}{1-xx_{k}}$ の $n-1$ 次までの係数の計算に等しく、適切な順序で通分することにより $O\left( m(\log m)^2 +n\log n \right)$ の演算コストで計算できます。

転置原理によると、この通分のアルゴリズムの基本操作をすべて転置し、マージの逆順、すなわち分割するような順番で計算することで、今度は多点評価が計算されます。この方法は、一般的な実装において、多項式除算を用いて多点評価を直接解く方法^(*1)よりも定数倍で効率的です。

• Library Checker「Multipoint Evaluation」
• 37zigenのHP 「Multipoint Evaluation の アルゴリズム」

(*1) 37zigenのHP 「Multipoint Evaluation の アルゴリズム」 の最初のアルゴリズムを参考にしてください。

補間多項式 ←→ 部分分数分解

多点評価 $\bm{y}=V\bm{f}$ の逆 $\bm{f}=V^{-1}\bm{y}$ は補間多項式の計算に相当します。これの転置は $\bm{v}=(V^T)^{-1}\bm{w}$ ですが、それは $\displaystyle\sum_{k=0}^{n} \frac{v_k}{1-xx_{k}}$ の逆の計算であるため部分分数分解^(*1)に相当します。

(*1) 部分分数分解問題は maspyのHP「[多項式・形式的べき級数] 高速に計算できるものたち」 より。「Vandermonde 行列の作用」では、ヴァンデルモンド行列で表した $4$ つの計算の関係が整理されています。

Bostan–Mori 法

LSB-first の Bostan–Mori 法は、 $n$ 項間線形漸化的数列の第 $K$ 項、あるいは FPS で表せば $[x^K]\dfrac{P(x)}{Q(x)}$ の値を計算するアルゴリズムです。 FFT による畳み込みをベースとするとき、演算コストを $\sim \dfrac{2}{3}M(n)\log_2 K$ ^(*2)（ $M(n)$ は $n$ 次多項式どうしの積の計算の演算コスト ^(*1)）とすることができます。

初項を入力 $\bm{v}$ とすれば、線形漸化的数列の第 $K$ 項は $\bm{v}$ の要素の線形結合（前述の、重み和）で表されます。

$$\begin{pmatrix}w\end{pmatrix}=\begin{pmatrix}W_0 & W_1 & \cdots & W_{n-1} \end{pmatrix} \begin{pmatrix}v_0 \cr v_1 \cr \vdots \cr v_{n-1} \end{pmatrix}$$

転置原理によると、 $W_0, W_1, \cdots , W_{n-1}$ の値は同じ演算コスト $\sim\dfrac{2}{3}M(n)\log_2 K$ で得られます。計算順が逆になるため、これは MSB-first のアルゴリズムとなります。この計算結果から、線形漸化的数列の連続する $n$ 項の値を求めることができます。

• Library Checker「Kth term of Linearly Recurrent Sequence」
• Library Checker「Consecutive Terms of Linear Recurrent Sequence」
• Bostan, Alin, and Ryuhei Mori. “A simple and fast algorithm for computing the N-th term of a linearly recurrent sequence.” Symposium on Simplicity in Algorithms (SOSA). Society for Industrial and Applied Mathematics, 2021. (arXiv)
• 「線形漸化的数列のN項目の計算」 (@ryuhe1(Ryuhei Mori) より)
• 「X^N mod P(X) の計算」 (@ryuhe1(Ryuhei Mori) より)

(*1) 不正確かもしれませんが、今回は「 $n$ 以上で最小の $2$ 冪の整数を $2^k$ とするとき、 $M(n)$ は長さ $2^k$ の FFT $6$ 回分」に相当するとします。
(*2) 詳細な最適化がなされた場合の演算コストです。

冪級数合成 (power series composition) ←→ power projection

$f$ を多項式とするとき、 $h=f(g)$ を計算することを考えます。 $g$ が FPS であって定数項が $0$ ( $[x^0]g(x)=0$ ) であるとき、 $f$ を入力 $\bm{v}$ とした計算は行列-ベクトル積で表せます。

$$\bm{w}=\begin{pmatrix} [x^0]h \cr [x^1]h \cr \vdots \cr [x^{n-1}]h \end{pmatrix}=\begin{pmatrix}[x^0]g^0 & [x^0]g^1 & \cdots & [x^0]g^{n-1} \cr[x^1]g^0 & [x^1]g^1 & \cdots & [x^1]g^{n-1} \cr\vdots & \vdots & \ddots & \vdots \cr [x^{n-1}]g^0 & [x^{n-1}]g^1 & \cdots & [x^{n-1}]g^{n-1} \cr\end{pmatrix}\begin{pmatrix} [x^0]f \cr [x^1]f \cr \vdots \cr [x^{n-1}]f \end{pmatrix}$$

この問題の転置問題は次で表されます。

$$ \bm{y} =\begin{pmatrix}[x^0]g^0 & [x^1]g^0 & \cdots & [x^{n-1}]g^0 \cr[x^0]g^1 & [x^1]g^1 & \cdots & [x^{n-1}]g^1 \cr\vdots & \vdots & \ddots & \vdots \cr [x^0]g^{n-1} & [x^1]g^{n-1} & \cdots & [x^{n-1}]g^{n-1} \cr\end{pmatrix} \bm{x}$$

この問題は power projection と呼ばれます。 FPS で表現すれば、 power projection は $h(y)=[x^{n-1}] \dfrac{f(x)}{1-g(x)y}$ の計算に相当します。さらにこれは $O(n(\log n)^2)$ 時間で計算でき、したがって FPS の合成および power projection はいずれも $O(n(\log n)^2)$ 時間で計算できることがわかります。導出・実装方法について詳しい解説があるのでそれを参考にして下さい。

power projection の計算によって FPS の合成逆元が得られます。

• Library Checker「Composition of Formal Power Series (Large)」
• Library Checker「Compositional Inverse of Formal Power Series (Large)」
• “[Tutorial] Generating Functions in Competitive Programming (Part 2)” by zscoder (“Coefficient of fixed $x^k$ in $f(x)^i$ の項)
• maspyのHP「FPS 合成・逆関数の解説（１）逆関数と Power Projection」
• maspyのHP 「FPS 合成・逆関数の解説（2）転置原理による合成アルゴリズムの導出」

多項式 $f$ と集合冪級数^(*1) $s$ が与えられるときの合成 $h=f(s)$ は、 $s$ の定数項が $0$ のとき、下図のような手順で $O(n^22^n)$ 時間で計算できます。^(*2)

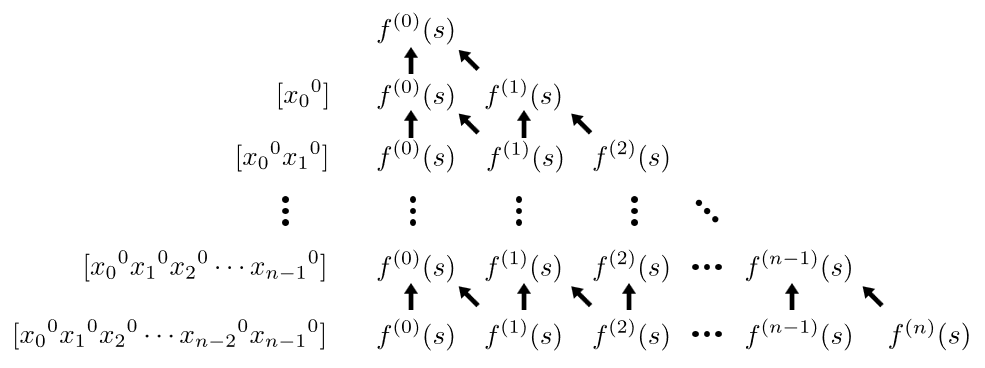
合成を転置した問題である power projection は、 $h(y)=[x_0x_1\cdots x_{n-1}] \dfrac{t}{1-sy}$ ( $t$ は集合冪級数 , $h$ は高々 $n$ 次の多項式) と表せます。 power projection の計算は

• $n$ 頂点のグラフの彩色多項式の計算や
• $2n$ 頂点のグラフのマッチングの数え上げ

に応用があります。

• Library Checker「Power Projection of Set Power Series」
• Library Checker「Polynomial Composite Set Power Series」
• Optimal Algorithm on Polynomial Composite Set Power Series by Elegia
• maspyのHP「集合べき級数関連 (4) 問題例」

(*1) 集合冪級数とは、 $n$ 変数の FPS に対してすべての変数で $\mod {x_k}^2$ （つまり、 $2$ 次以上を切り捨てる）としたものです。データとしては $2^n$ 個の係数で表現され、乗法の計算は subset convolution です。
(*2) 理論としては下から上へ、実装としては右から左へ、という順にみると見通しがよいと思います。

他の変換

さらに多くの例を示す表を含んだ、 Alin Bostan による資料があります^(*1)。ただしフランス語で簡潔に書かれていて理解が難しかったので、今できる範囲でなんとか補足説明をしようと思います。

• 資料[A] Bostan, Alin. “Algorithmes rapides pour les polynômes, séries formelles et matrices.” Les cours du CIRM 1.2 (2010): 75-262. p.218 (pdf では 145 ページ目)

多項式の Taylor Shift ( P(x) → P(x+1) ) ←→ 二項変換

$a_{ij}={}_i\mathrm{C}_j$ （二項係数、ただし $i\lt j$ のとき ${}_i\mathrm{C}_j=0$ とする）とすれば、 $\bm{w}=A\bm{v}$ は単純二項変換^(*2)です。一方、 $\bm{y}=A^T\bm{x}$ は多項式 $P(x)$ の係数が与えられたときに二項定理に基づいて $P(x+1)$ の係数を求める計算です。それぞれ逆変換は交代二項変換と $P(x-1)$ の計算です。

二項変換は下降冪級数の $x=0,1,2,\ldots$ における評価とほぼ同じです。この概念の説明は別の投稿^(*3)を参照してください。また、二項変換は指数型母関数における $e^x$ の乗算、あるいは通常型母関数の操作でも表現されます^(*2)。

資料[A]ではこれの $q$-類似(であろう)項目が含まれていますが、私は問題形式・計算内容を把握できませんでした。

• Library Checker 「Polynomial Taylor Shift」

多項式の評価点シフト ←→ 多項式 mod (x-1)^n

$n-1$ 次以下の多項式 $f$ について FPS $P(x)=\sum_{k=0}^{\infty}x^kf(k)$ を考えると、高々 $n-1$ 次の多項式 $Q(x)$ が存在して $P(x)=\dfrac{Q(x)}{(1-x)^n}$ が成り立ちます。

よって、 $f(0),f(1),\ldots ,f(n-1)$ が与えられているとき、 $f(n)$ 以降の値すなわち $P(x)$ の $n$ 次以上の係数はある線形漸化式に従って順に計算できます。この計算過程を転置すると、 Bostan–Mori 法のときと同様に考えることで、係数列が与えられた多項式に対して $\text{mod}\; (x-1)^n$ での剰余の計算が得られます。

• Library Checker 「Shift of Sampling Points of Polynomial」
• maspyのHP「[多項式・形式的べき級数] 高速に計算できるものたち」 「$\sum_{n=0}^{N} n^kr^n$, $\sum_{n=0}^{\infty} n^kr^n$」の項

(*1) Twitter で教えていただきました。 Thank you hly1204: https://twitter.com/yeye39618806/status/1784568483969487153 フランス語なのでやはり難度は高いと思いますが、トピックの回収のためには強力かもしれません。本投稿では競プロ向けの解説ということで転置原理の章のすべてのトピックを調査するということはしていません。
(*2) 参考：しょぼんブログ「連載 しょぼんコーダー 6 一般化された包除原理と二項変換」
(*3) Mathenachia「yukicoder Paint and Fill 解法詳細解説」 「（制約２）多項式の評価点シフト」

おわり