はじめに
yukicoder で開催された Advent Calendar Contest 2021 の 25 日目、最終問題を担当させていただきました。 Nachia でございます。クリスマスといえばツリー、ツリーといえば木上のクーロン!ということで、木上の距離に従ってクーロンの法則を考える問題を出題しました。お楽しみいただけたでしょうか。(ネタがネタなので、所謂ワクワクだったかもしれません……)
問題はこちら↓↓↓

以降、「木上のクーロン」はこの問題を指します。
今回は、「木上のクーロン」に似た問題を $4$ 問挙げ、問題集を作りました。「木上のクーロン」の想定解法の理解を前提としますが、まだ実装できていない方も楽しめますので、ぜひとも最後までよろしくお願いいたします。
「木上のクーロン」補遺
レベルの設定は ★5.0 とも考えていましたが、すでにアドベコンで出題された問題たちが難しすぎたので、相対的に ★4.5 と判断しました。これより低くしなかった一番の理由は、仮に知識によって考察がすぐに終わったとしてもその後の実装が難しいだろうと考えたことです。
動機
- 似た問題を作りすぎたこと。
ルール
- ジャッジや実装例を用意しているとは限りません。
- 解法の評価基準は、 $N$ に対する最悪計算量オーダーの小ささとします。定数倍は一概に大きく、競プロにおいて現実的な範囲では $O(N^2)$ や $O(N\sqrt{N})$ 時間の解法のほうが早く求まるかもしれませんが、例えば $O(N (\log N)^5)$ 時間の解法のほうが優れているものとします。
- 求める値は有理数となるので、 $\bmod P$ で求めて出力してください。 $P=998244353$ と考えてかまいません。
- 問題サイズが非常に大きい場合に生じる課題(例えば入力長を表す整数が $32$ ビットに収まらない場合や、 $998244353\leq N$ のときで $0$ 除算が発生する場合)のことはいったん忘れます。計算量は普段の競プロと同様に考えます。
- $N$ 次多項式どうしの積の各項の係数(係数は $\bmod P$ で考える)は計算量 $O(N \log N)$ で求まるものとします。
- $N$ 頂点のグラフは、頂点に $1,2, \ldots ,N$ の番号が振られています。また、木の $2$ 頂点 $u,v$ 間の単純パスに含まれる辺の個数を $\text{dist}(u,v)$ と表します。
- $\Theta(N^2)$ 個の単純パスに関する問題です。
- 多項式の不定元には原則 $X$ を用います。(なんとなくかっこいいので)
本番
対 戦 よ ろ し く お 願 い し ま す
第 $1$ 問(~★4.5)
(出典: Library Checker)
この問題をまだ解いていなかった方は、「木上のクーロン」でかなり苦戦されたのではないでしょうか。
出典の問題では厳密な値が要求されますが、この記事ではルールに則り $\bmod P$ で考えます。
問題文
$N$ 頂点の木が与えられます。次の多項式の $N-1$ 次以下の項それぞれの係数を求めてください。
$$P(X)=\sum_{u=1}^{N-1} \sum_{v=u+1}^N X^{\text{dist}(u,v)}$$
解説
想定解
計算量 $O(N (\log N)^2)$ のアルゴリズムが存在します。
木上のすべての単純パスに関する問題なので、重心分解をすると、重心を通る単純パスのみを考える問題に変換できます。
重心が端点となるような単純パスについては線形時間で求めてもよいです。すると、考えるパスはすべて $p \rightarrow g \rightarrow q$ $(p \neq g, q \neq g)$ の形で表せます。このとき、 $\text{dist}(p,q)=\text{dist}(p,g)+\text{dist}(g,q)$ です。
このようなときに有用なのが畳み込みの計算です。頂点数 $n$ の木が重心 $g$ によって $2$ つの部分木に分割されるとします。 $2$ つの部分木それぞれについて、 $X^k$ の係数を $\text{dist}(g,p)=k$ となる頂点 $p$ の個数とした多項式を考えると、 $2$ つの多項式の積は単純パスの長さごとの数え上げとなり、これこそ求めるものです。 $2$ つの多項式は幅優先探索で計算量 $O(n)$ で求まり、その積は計算量 $O(n \log n)$ で求まります。
重心によって $3$ つ以上の部分木に分割されるときはより複雑ですが、次の $2$ 通りの対処方法が考えられます。
- 次数の小さい順に並べ、前から足し合わせながら順に計算する。
$ab+ac+bc=ab+(a+b)c$ のような考え方。 - 「木上のクーロン」同様、全体から部分を引き、 $\frac{1}{2}$ 倍する。
$(a+b+c)^2-a^2-b^2-c^2=2(ab+ac+bc)$ のような考え方。
どちらも、対象の木の頂点数 $n$ に対して計算量 $O(n \log n)$ ですが、一般に前者のほうが定数倍が大きくないです。
重心分解後のサイズ $n$ の問題が計算量 $O(n \log n)$ で解けるので、全体の計算量は $O(N (\log N)^2)$ となります。
実装例
出展をご参照ください。
第 $2$ 問(~★5.0)
(自作)
問題文
$N$ 頂点の木が与えられます。 $\text{dist}(1,u)$ が偶数となるような $u$ の集合を $S$ とします。ここで、次の多項式の $N-1$ 次以下の項それぞれの係数を求めてください。
$$P(X)=\sum_{u \in S} \sum_{v \in S} X^{\text{dist}(u,v)}$$
ヒント
考察 $1$
この問題は 第 $1$ 問 同様 $\Theta(N^2)$ 個の単純パスの長さの度数分布を求める問題となります。ただし、木には数え上げないパスもあることに注意してください。今回は、問題を一般化し、パスの端点に関して重みをつけて数え上げる問題を考えるとよいです。
解説
想定解
計算量 $O(N (\log N)^2)$ のアルゴリズムが存在します。
第 $2$ 問 は、次の問題の具体例といえます。
問題 $2.1$
$N$ 頂点の木と数列 $ \{ A_i \} _{i=1}^N, \{ B_i \} _{i=1}^N$ が与えられます。次の多項式の $N-1$ 次以下の項それぞれの係数を求めてください。
$$P(X)=\sum_{u=1}^N \sum_{v=1}^N A_u B_v X^{\text{dist}(u,v)}$$
第 $2$ 問 について、 $S$ に含まれる番号の頂点に $1$ 、その他の頂点に $0$ の重みを振ると考えると、問題 $2.1$ の答えから 第 $2$ 問 の答えが得られます。
問題 $2.1$ は、 第 $1$ 問 と同様の方法で解けます。解法の途中で、重心 $g$ との距離の度数分布を求めますが、これを重み付きで求めます。さらに $A_i,B_i$ を交換した場合と $u=v$ の場合を計算します。
解説補遺
この問題は、次の問題のクエリすべてについて答えの度数分布を求めるための問題と捉えることもできます。
実装例
第 $3$ 問(~★5.5)
(自作)
問題文
$N$ 頂点の木が与えられます。時刻 $0$ に各頂点にスライムが出現し、移動を始めます。このとき頂点 $i$ に出現するスライムの質量は $M_i$ として与えられます。異なる頂点に出現したスライムどうしの動きは独立に考えます。スライムは、今いる頂点から $1$ 単位時間でちょうど隣接する頂点まで移動します。頂点にさしかかったとき、頂点に入ってくるときに通った辺以外の隣接する辺に均等に分散しますが、ここで対象の辺が存在しないとき、スライムは消滅します。スライムが時刻 $t$ にある頂点に到達し、直後に消滅した場合、時刻 $t$ にはそのスライムは残っているものとして扱います。時刻 $t$ のスライムの質量 $1$ あたりの価値は $V_t$ です。時間は時刻 $N$ まで考えます。
$2$ つの小課題があります。
(小課題A) $t=0,1,2, \ldots ,N$ について、時刻 $t$ 時点で残っているスライムの総質量を求めてください。
(小課題B) $p=1,2, \ldots ,N$ について、頂点 $p$ に到達するスライムの総価値を求めてください。ただし、スライムの価値は頂点 $p$ に通過した瞬間での価値を用いて計算します。
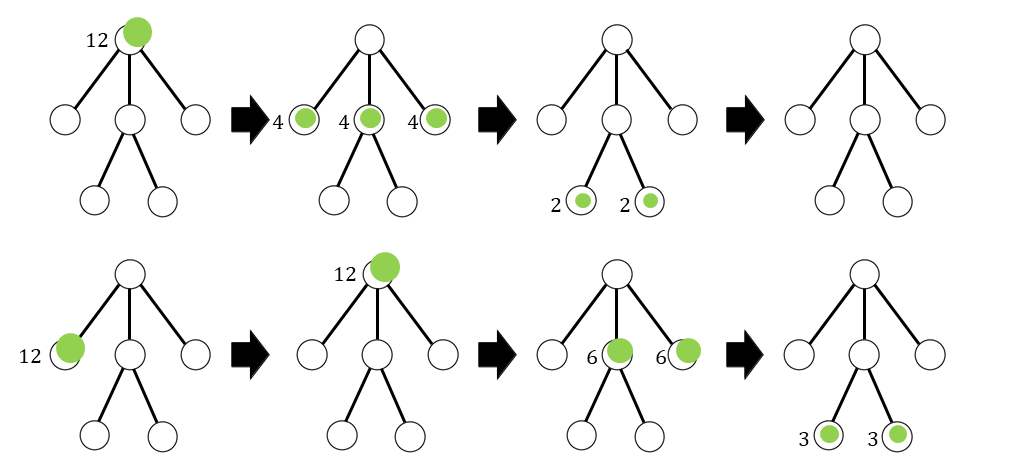
ヒント
(小課題AB共通) 考察 $1$
$f_I(u,v)$ を、頂点 $u$ に出現して移動を始めた質量 $1$ のスライムのうち、頂点 $v$ に到達するスライムの質量とします。
$f_O(u,v)$ を、頂点 $u$ に頂点 $v$ から遠い側から到達して移動を始めた質量 $1$ のスライムのうち、頂点 $v$ に到達するスライムの質量とします。
重心分解でうまく求められる形にするために、重心 $g$ をとったときに各頂点 $p$ について $f_I(p,g),f_I(g,p),f_O(g,p)$ を求めます。
木 $T$ に含まれるある頂点 $g$ とすべての頂点 $p$ についての $f_I(p,g),f_I(g,p),f_O(g,p)$ は $T$ の頂点数に関する線形時間で計算できます。
(小課題AB共通) 考察 $2$
異なる $3$ 頂点 $a,b,c$ があって、 $a,c$ 間の単純パスに $b$ が含まれるとき、
$$f_I(a,c)=f_I(a,b)f_O(b,c)$$
が成り立ちます。
解説
(小課題A)想定解
計算量 $O(N(\log N)^2)$ のアルゴリズムが存在します。
ヒント 中で定義した $f_I(u,v),f_O(u,v)$ を使います。
$t=1,2, \ldots ,N$ について、時刻 $t$ に葉の頂点に到達して消滅するスライムの総質量を求め、全体から順に引けばよいです。
第 $3$ 問(小課題A) は、次の問題の具体例といえます。
問題 $3.1$
$N$ 頂点の木と関数 $f_I(u,v),f_O(u,v)$ 、数列 $ \{ A_i \} _{i=1}^N, \{ B_i \} _{i=1}^N$ が与えられます。 $3$ 頂点 $a,b,c$ があって、 $a,c$ 間の単純パスに $b$ が含まれるとき、 $f_I(a,c)=f_I(a,b)f_O(b,c)$ が成り立ちます。また、任意の部分木の頂点集合 $T$ と部分木内の頂点 $g$ が与えられたとき、すべての $p \in T$ について $f_I(g,p),f_O(p,g)$ を計算量 $O(|T|)$ で求められます。次の多項式の $N-1$ 次以下の項それぞれの係数を求めてください。
$$P(X)=\sum_{u=1}^N \sum_{v=1}^N A_uB_vf_I(u,v) X^{\text{dist}(u,v)}$$
問題の条件をこのようにしても、木のすべての頂点 $p$ についての $f_I(p,g)$ は線形時間で求まることに注意します。
重心分解によって、 $u,v$ 間の単純パスが頂点 $g$ を通る場合のみを考える問題に変形します。 $u=g$ または $v=g$ の場合を別で計算しておくことで、この場合を除きます。 $g$ によって分かれる部分木を区別せずに計算し、その後、重複分を各部分木で計算します。すると、次の問題が残ります。
問題 $3.2$
次の多項式の $N-1$ 次以下の項それぞれの係数を求めてください。
$$P(X)=\sum_{u=2}^N \sum_{v=2}^N A_uB_vf_I(u,1)f_O(1,v) X^{\text{dist}(u,1)+\text{dist}(1,v)}$$
$$P(X)= \left( \sum_{u=2}^N A_u f_I(u,1) X^{\text{dist}(u,1)} \right) \left( \sum_{v=2}^N B_v f_O(1,v) X^{\text{dist}(1,v)} \right) $$
より、問題 $3.2$ は計算量 $O(N \log N)$ で解けます。
従って、問題 $3.1$ は計算量 $O(N (\log N)^2)$ で解けます。
(小課題B)想定解
計算量 $O(N (\log N)^2)$ のアルゴリズムが存在します。
ヒント 中で定義した $f_I(u,v),f_O(u,v)$ を使います。
第 $3$ 問(小課題B) は、次の問題の具体例といえます。
問題 $3.3$
$N$ 頂点の木と関数 $f_I(u,v),f_O(u,v)$ 、数列 $ \{ A_i \} _{i=1}^N, \{ B_i \} _{i=1}^N, \{ V_i \}_{i=0}^{N-1}$ が与えられます。 $3$ 頂点 $a,b,c$ があって、 $a,c$ 間の単純パスに $b$ が含まれるとき、 $f_I(a,c)=f_I(a,b)f_O(b,c)$ が成り立ちます。また、任意の部分木の頂点集合 $T$ と部分木内の頂点 $g$ が与えられたとき、すべての $p \in T$ について $f_I(g,p),f_O(p,g)$ を計算量 $O(|T|)$ で求められます。 $v=1,2, \ldots ,N$ について、以下の値を求めてください。
$$E_v=\sum_{u=1}^N A_uB_vf_I(u,v) V_{\text{dist}(u,v)}$$
問題の条件をこのようにしても、木のすべての頂点 $p$ についての $f_I(p,g)$ は線形時間で求まることに注意します。
重心分解によって、 $u,v$ 間の単純パスが頂点 $g$ を通る場合のみを考える問題に変形します。 $u=g$ または $v=g$ の場合を別で計算しておくことで、この場合を除きます。 $g$ によって分かれる部分木を区別せずに計算し、その後、重複分を各部分木で計算します。すると、次の問題が残ります。
問題 $3.4$
$v=2,3, \ldots ,N$ について、以下の値を求めてください。
$$E_v=\sum_{u=2}^N A_uB_vf_I(u,1)f_O(1,v) V_{\text{dist}(u,1)+\text{dist}(1,v)}$$
$\{ V_i \}_{i=0}^{N-1}$ に任意の値を追加して $\{ V_i \}_{i=0}^{2N+1}$ とし、多項式 $P(X)$ の $X^e$ の係数を $[X^e](P(X))$ と表すと、
$$E_v = B_v f_O(1,v) [X^{N+\text{dist}(1,v)}] \left( \sum_{u=2}^N A_u f_I(u,1) X^{N-\text{dist}(u,1)} \right) \left( \sum_{d=2}^{2N+1} V_d X^{d} \right) $$
が成り立ちます。よって、問題 $3.4$ は計算量 $O(N \log N)$ で解けます。
従って、問題 $3.3$ は計算量 $O(N (\log N)^2)$ で解けます。
解説補遺
(小課題A) が距離の度数分布の形式で、 (小課題B) が「木上のクーロン」と同じ形式です。
(小課題B) について、価値ではなく質量を求めることにすれば、計算途中でスライムが移動した距離の情報が不要になります。このときは全方位木 DP が効率的で計算量を $O(N)$ とできます。
実装例
(小課題A):https://github.com/NachiaVivias/tree-coulomb-variety/blob/main/source/problem-3A/main.cpp
(小課題B):https://github.com/NachiaVivias/tree-coulomb-variety/blob/main/source/problem-3B/main.cpp
第 $4$ 問(~★5.5)
(原案:「木上のクーロン」 tester の Nyaan さん、アルゴリズム提案: Nachia)
元の問題「木上のクーロン」に更新・求値クエリを追加した問題です。
問題文
$N$ 頂点の木が与えられます。はじめ、 $Q_i=0$ $(1 \leq i \leq N)$ です。 合計 $K= \Theta (N)$ 個のクエリを処理してください。ただし、すべてのクエリが最初に一括で与えられます。
- 更新 $(p,q)$ : $Q_p \leftarrow q$ 。
- 求値 $(p)$ : $E_p=\sum_{i=1}^{N} \frac{(N!)^2Q_i}{(\text{dist}(p,i)+1)^2}$ の値を求めてください。
ヒント
考察 $1$
「木上のクーロン」と同様に、問題を分解します。
木を重心分解します。木全体の計算結果から部分木を往復するような部分の計算結果を引く方法も使います。
考察 $2$
クエリ列を分割統治することで、すべての更新クエリを事前に実行するような問題に変換できます。なお、問題サイズは増加します。
考察 $3$
分割された各問題で求める値は、いくつかの $X$ に対する
$$\sum_i \frac{C_i}{(D_i+X)^2}$$
の値、と表せます。
想定解
想定解
計算量 $O(N (\log N)^4)$ のアルゴリズムが存在します。
考察の階層の深い順に解説します。
問題 $4.1$
整数列 $\{ C_i \} _{i=1}^{k}, \{ D_i \} _{i=1}^{k}, \{ X_i \} _{i=1}^{q}$ が与えられます。 $0 \leq D_i \leq n-1$ と $0 \leq X_i \leq n+1$ を満たします。関数 $f(X)$ を次で定義します。
$$f(X)=\sum_{i=1}^k \frac{C_i}{(D_i+X)^2}$$
$q$ 個の値 $f(X_1),f(X_2), \ldots , f(X_q)$ を計算量 $O(q(\log q)^2+k (\log k)^2)$ で求めてください。
$f(X)$ の分子と分母をそれぞれ多項式として分割統治法で計算し、その後多点評価を行います。
(多点評価の参考: https://37zigen.com/multipoint-evaluation/ )
「木上のクーロン」と同様の方法で求める、計算量 $O(n \log n)$ の方法もありますが、それを用いて計算量のオーダーを改善できなかったため、以降では特に利用しません。
問題 $4.2$
空の整数列 $C,D$ が与えられます。ここから、合計 $q$ 個のクエリを計算量 $O(q (\log q)^3)$ で処理してください。
- 追加 $(C_i,D_i)$ : $C,D$ の末尾にそれぞれ $C_i,D_i$ を追加する。
- 求値 $(X_i)$ : 関数 $f(X)$ を問題 $4.1$ と同様に定義し、 $f(X_i)$ の値を求める。
$2 \leq q$ のとき、クエリ列を前半と後半に分けます。計算すべき式の線形性より、問題を次の $3$ つに分けられます。
- 前半のみのクエリ列を処理する。
- 後半のみのクエリ列を処理する。
- 前半の追加クエリと後半の求値クエリのみを処理する。
ここで、 3. は問題 $4.1$ と同じであるため、計算量 $O(q (\log q)^2)$ で処理できます。従って、典型的な分割統治法より全体の計算量は $O(q (\log q)^3)$ となります。この方法はオフラインオンライン変換と呼ばれることがあります。(参考:https://qiita.com/tmaehara/items/0687af2cfb807cde7860)
さて、 第 $4$ 問 で与えられた木を「木上のクーロン」同様に重心分解し、式変形すると、元の問題は $q$ の総和が $O(K \log N)$ であるような問題 $4.2$ の集まりに変形できます。従って、この問題を計算量 $O(N (\log N)^4)$ で解くことができました。
解説補遺
$K=o(N)$ のときはクエリの個数で重みづけして木を重心分解すると、計算量を $O(N\log N+K (\log K)^4)$ とできます。
$K=\Omega(N)$ のときは $K=O(N)$ の問題に適切に分割すると、全体の計算量を $O(K (\log N)^4)$ とできます。
実装例
おわりに
お気づきかもしれませんが、これは「机上の空論」問題集です。大して役に立ちませんよね。
(終)